数据结构 基础

摘要

JDK：1.8.0_202

一：数组

数组对应的英文是array，是有限个相同类型的变量所组成的有序集合，数组中的每一个变量被称为元素。

1.1 内存存储格式

Q：数组在内存中的顺序存储，具体是什么样子呢？

内存是由一个个连续的内存单元组成的，每一个内存单元都有自己的地址。在这些内存单元中，有些被其他数据占用了，有些是空闲的。

数组中的每一个元素，都存储在小小的内存单元中，并且元素之间紧密排列，既不能打乱元素的存储顺序，也不能跳过某个存储单元进行存储。

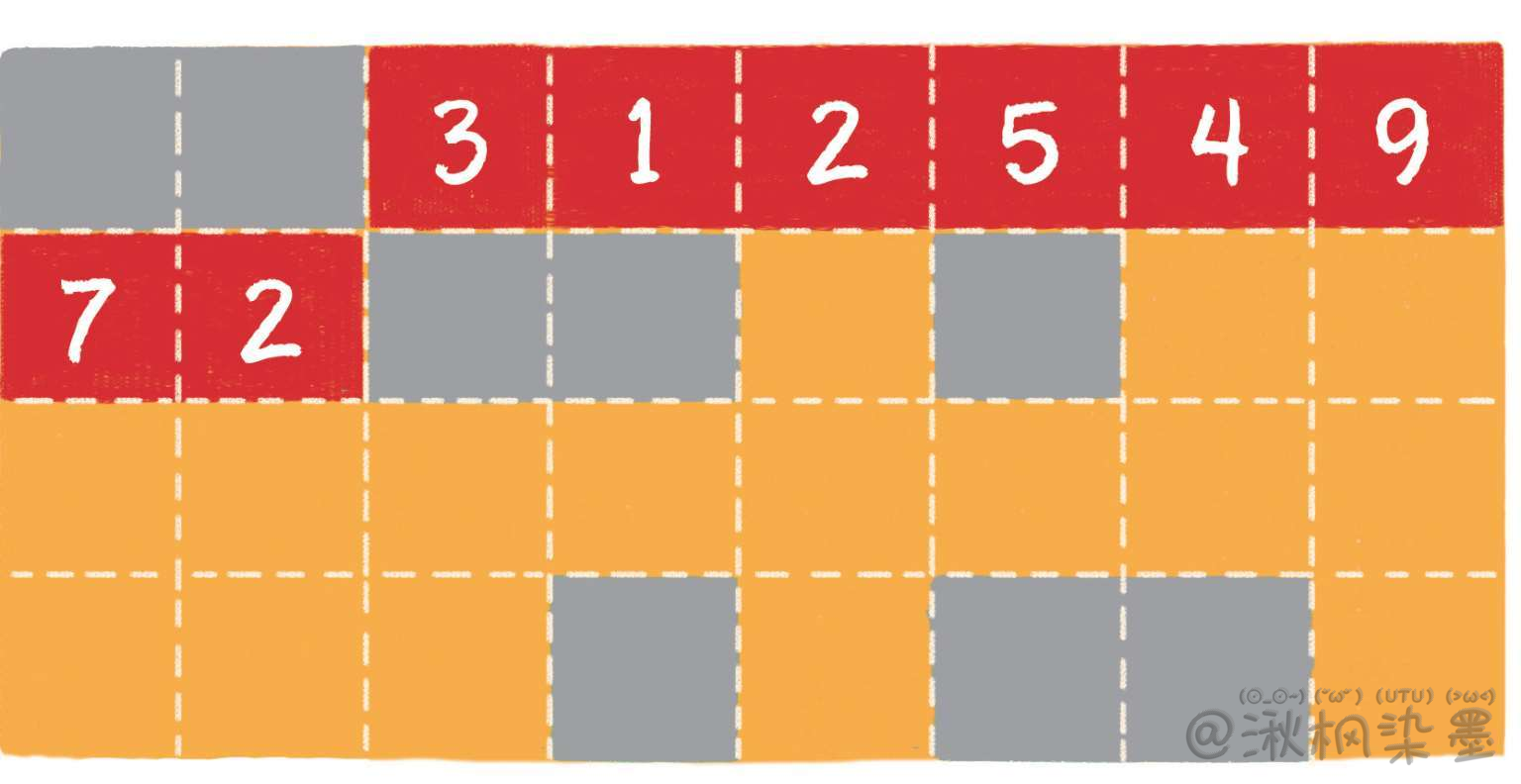
在上图中，橙色的格子代表空闲的存储单元，灰色的格子代表已占用的存储单元，而红色的连续格子代表数组在内存中的位置。

不同类型的数组，每个元素所占的字节个数也不同，上图只是一个简单的示意图。

1.2 基本操作

1. 读取元素

int[] array = new int[]{3, 1, 2, 5, 4, 9, 7, 2};
// 输出数组下标为3的元素
System.out.println(array[3]);	// 5

2. 更新元素

int[] array = new int[]{3, 1, 2, 5, 4, 9, 7, 2};
// 给数组下标为5的元素赋值
array[5] = 10;
// 输出数组下标为5的元素
System.out.println(array[5]);	// 10

3. 插入元素

由于数组的每一个元素都有其固定下标，所以不得不首先把插入位置及后面的元素向后移动，腾出地方，再把要插入的元素放到对应的数组位置上。

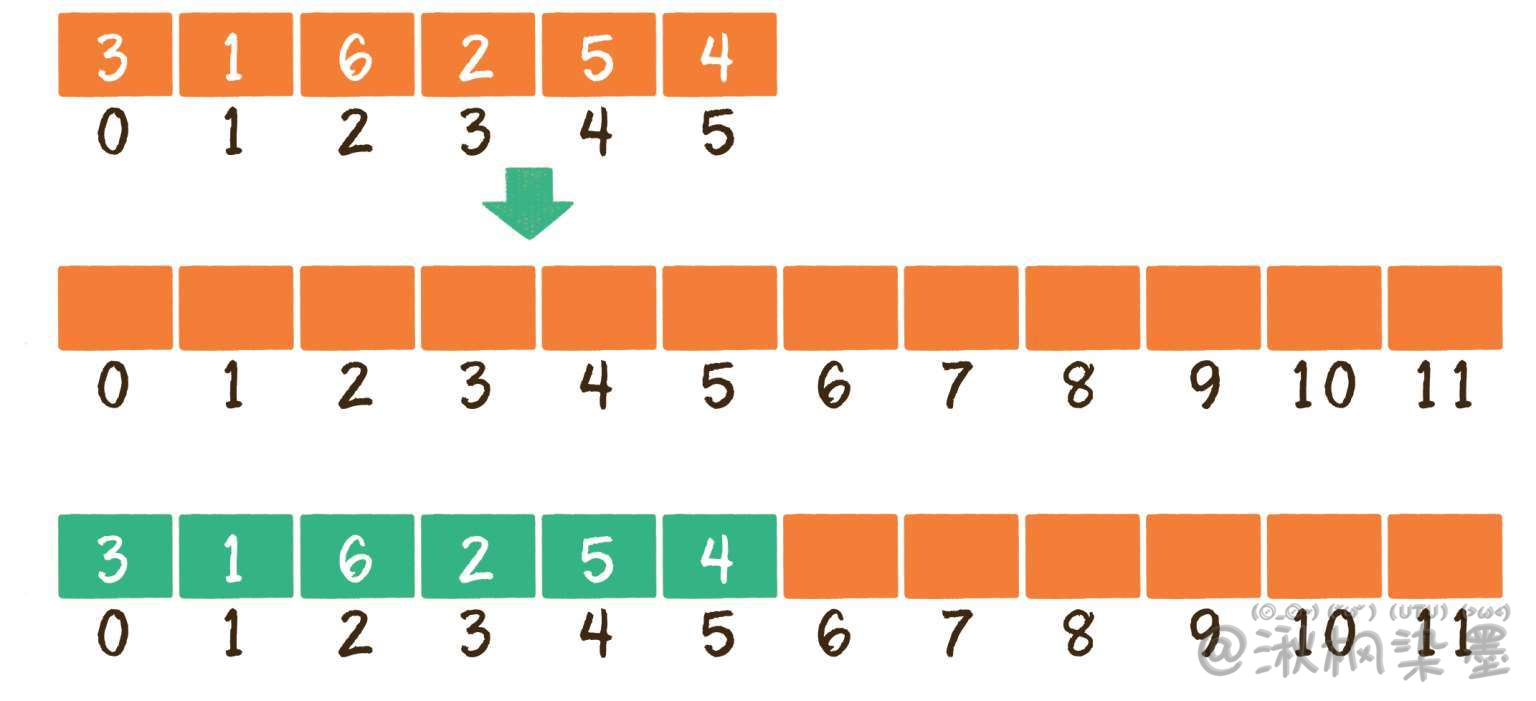
如果满元素，就需要扩容了。不过数组的长度在创建时就已经确定了，此时可以创建一个新数组，长度是旧数组的2倍，再把旧数组中的元素统统复制过去，这样就实现了数组的扩容。

public class ArrayTest {

    private int[] array;

    private int size;

    public ArrayTest(int capacity) {
        this.array = new int[capacity];
        this.size = 0;
    }

    /**
     * 数组插入元素
     *
     * @param element 插入的元素
     * @param index   插入的位置
     * @throws Exception IndexOutOfBoundsException
     */
    public void insert(int element, int index) throws Exception {
        // 判断访问下标是否超出范围
        if (index < 0 || index > size) {
            throw new IndexOutOfBoundsException("超出数组实际元素范围");
        }

        // 如果实际元素达到数组容量上限，则对数组进行扩容
        if (size >= array.length) {
            resize();
        }

        // 从右向左循环，将元素逐个向右挪一位
        for (int i = size - 1; i >= index; i--) {
            array[i + 1] = array[i];
        }

        // 腾出的位置放入新元素
        array[index] = element;
        size++;
    }

    /**
     * 数组扩容
     */
    public void resize() {
        int[] arrayNew = new int[array.length * 2];
        // 从旧数组复制到新数组
        System.arraycopy(array, 0, arrayNew, 0, array.length);
        array = arrayNew;
    }

    /**
     * 输出数组
     */
    public void output() {
        System.out.println(Arrays.toString(array));
    }

    public static void main(String[] args) throws Exception {
        ArrayTest arrayTest = new ArrayTest(4);
        arrayTest.insert(3, 0);
        arrayTest.insert(7, 1);
        arrayTest.insert(9, 2);
        arrayTest.insert(5, 3);
        arrayTest.insert(6, 1);
        arrayTest.output(); // [3, 6, 7, 9, 5, 0, 0, 0]
    }

}

4. 删除元素

数组的删除操作和插入操作的过程相反，如果删除的元素位于数组中间，其后的元素都需要向前挪动1位。

/**
 * 数组删除元素
 *
 * @param index 删除的位置
 * @return 删除的元素
 */
public int delete(int index) throws Exception {
    //判断访问下标是否超出范围
    if (index < 0 || index >= size) {
    	throw new IndexOutOfBoundsException("超出数组实际元素范围！");
    }

    int deletedElement = array[index];

    //从左向右循环，将元素逐个向左挪1位
    for (int i = index; i < size - 1; i++) {
    	array[i] = array[i + 1];
    }

    size--;
    return deletedElement;
}

1.3 优劣势

优点：

具有非常高效的随机访问能力，只要给出下标，就能用常量时间找到对应元素。

缺点：

插入和删除。由于数组元素连续紧密地存储在内存中，插入、删除都会导致大量元素被迫移动，影响效率。

总的来说，数组所适合的是读操作多、写操作少的场景。

二：链表

2.1 单向链表

链表(linked list)是一种在物理上非连续、非顺序的数据结构，由若干节点(node)所组成。

单向链表的每一个节点又包含两部分，一部分是存放数据的变量data，另一部分是指向下一个节点的指针next。

private static class Node {
	int data;
	Node next;
}

• 链表的第1个节点被称为头节点；
• 最后1个节点被称为尾节点，尾节点的next指针指向空。

与数组按照下标来随机寻找元素不同，对于链表的其中一个节点A，只能根据节点A的next指针来找到该节点的下一个节点B，再根据节点B的next指针找到下一个节点C……

2.2 双向链表

双向链表比单向链表稍微复杂一些，它的每一个节点除了拥有data和next指针，还拥有指向前置节点的prev指针。

2.3 内存存储格式

链表则采用了见缝插针的方式，链表的每一个节点分布在内存的不同位置，依靠next指针关联起来。这样可以灵活有效地利用零散的碎片空间。

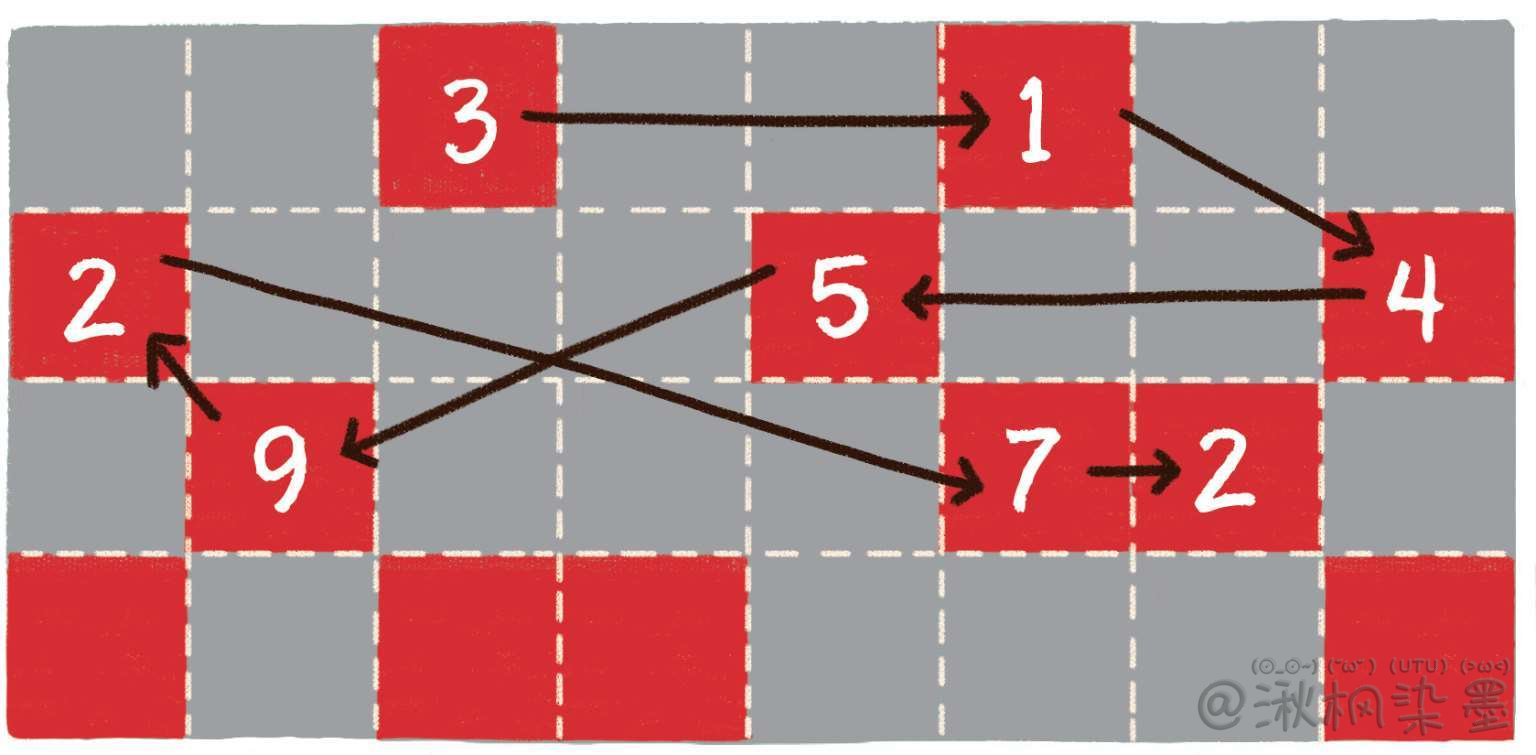
图中的箭头代表链表节点的next指针

2.4 基本操作

1. 查找节点

在查找元素时，链表不像数组那样可以通过下标快速进行定位，只能从头节点开始向后一个一个节点逐一查找。

2. 更新节点

如果不考虑查找节点的过程，链表的更新过程会像数组那样简单，直接把旧数据替换成新数据即可。

3. 插入节点

• 尾部插入：

  1. 把最后一个节点的next指针指向新插入的节点。

• 头部插入：

  1. 把新节点的next指针指向原先的头节点；
  2. 把新节点变为链表的头节点。

• 中间插入：

  1. 新节点的next指针，指向插入位置的节点；
  2. 插入位置前置节点的next指针，指向新节点。

3. 删除节点

• 尾部插入：

  1. 把倒数第2个节点的next指针指向空。

• 头部插入：

  1. 把链表的头节点设为原先头节点的next指针。

• 中间插入：

  1. 把要删除节点的前置节点的next指针，指向要删除元素的下一个节点。

许多高级语言，如Java，拥有自动化的垃圾回收机制，所以不用刻意去释放被删除的节点，只要没有外部引用指向它们，被删除的节点会被自动回收。

完整代码

public class MyLinkedList {

    // 头节点指针
    private Node head;
    // 尾节点指针
    private Node last;
    // 链表实际长度
    private int size;

    /**
     * 链表插入元素
     *
     * @param data  插入元素
     * @param index 插入位置
     */
    public void insert(int data, int index) throws Exception {
        if (index < 0 || index > size) {
            throw new IndexOutOfBoundsException(" 超出链表节点范围！");
        }
        Node insertedNode = new Node(data);
        if (size == 0) {
            //空链表
            head = insertedNode;
            last = insertedNode;
        } else if (index == 0) {
            //插入头部
            insertedNode.next = head;
            head = insertedNode;
        } else if (size == index) {
            //插入尾部
            last.next = insertedNode;
            last = insertedNode;
        } else {
            //插入中间
            Node prevNode = get(index - 1);
            insertedNode.next = prevNode.next;
            prevNode.next = insertedNode;
        }
        size++;
    }

    /**
     * 链表删除元素
     *
     * @param index 删除的位置
     */
    public Node remove(int index) throws Exception {
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException(" 超出链表节点范围！");
        }
        Node removedNode = null;
        if (index == 0) {
            //删除头节点
            removedNode = head;
            head = head.next;
        } else if (index == size - 1) {
            //删除尾节点
            Node prevNode = get(index - 1);
            removedNode = prevNode.next;
            prevNode.next = null;
            last = prevNode;
        } else {
            //删除中间节点
            Node prevNode = get(index - 1);
            Node nextNode = prevNode.next.next;
            removedNode = prevNode.next;
            prevNode.next = nextNode;
        }
        size--;
        return removedNode;
    }

    /**
     * 链表查找元素
     *
     * @param index 查找的位置
     */
    public Node get(int index) throws Exception {
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException(" 超出链表节点范围！");
        }
        Node temp = head;
        for (int i = 0; i < index; i++) {
            temp = temp.next;
        }
        return temp;
    }

    /**
     * 输出链表
     */
    public void output() {
        Node temp = head;
        while (temp != null) {
            System.out.print(temp.data + " ");
            temp = temp.next;
        }
    }

    /**
     * 链表节点
     */
    private static class Node {
        int data;
        Node next;

        Node(int data) {
            this.data = data;
        }
    }

    public static void main(String[] args) throws Exception {
        MyLinkedList myLinkedList = new MyLinkedList();
        myLinkedList.insert(3, 0);
        myLinkedList.insert(7, 1);
        myLinkedList.insert(9, 2);
        myLinkedList.insert(5, 3);
        myLinkedList.insert(6, 1);
        myLinkedList.remove(0);
        myLinkedList.output(); // 6 7 9 5
    }
}

2.5 数组VS链表

时间复杂度：

	查找	更新	插入	删除
数组	O(1)	O(1)	O(n)	O(n)
链表	O(n)	O(1)	O(1)	O(1)

从表格可以看出，数组的优势在于能够快速定位元素，对于读操作多、写操作少的场景来说，用数组更合适一些。相反地，链表的优势在于能够灵活地进行插入和删除操作，如果需要在尾部频繁插入、删除元素，用链表更合适一些。

三：栈和队列

3.1 栈

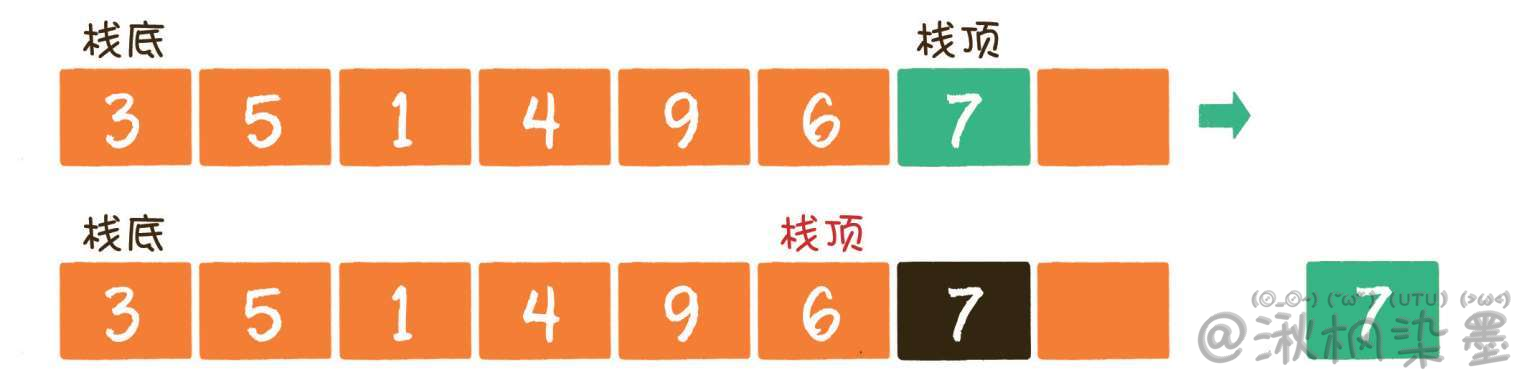
栈中的元素只能先入后出(First In Last Out，简称FILO)。最早进入的元素存放的位置叫作栈底（bottom），最后进入的元素存放的位置叫作栈顶（top）。

栈这种数据结构既可以用数组来实现，也可以用链表来实现。

3.2 基本操作

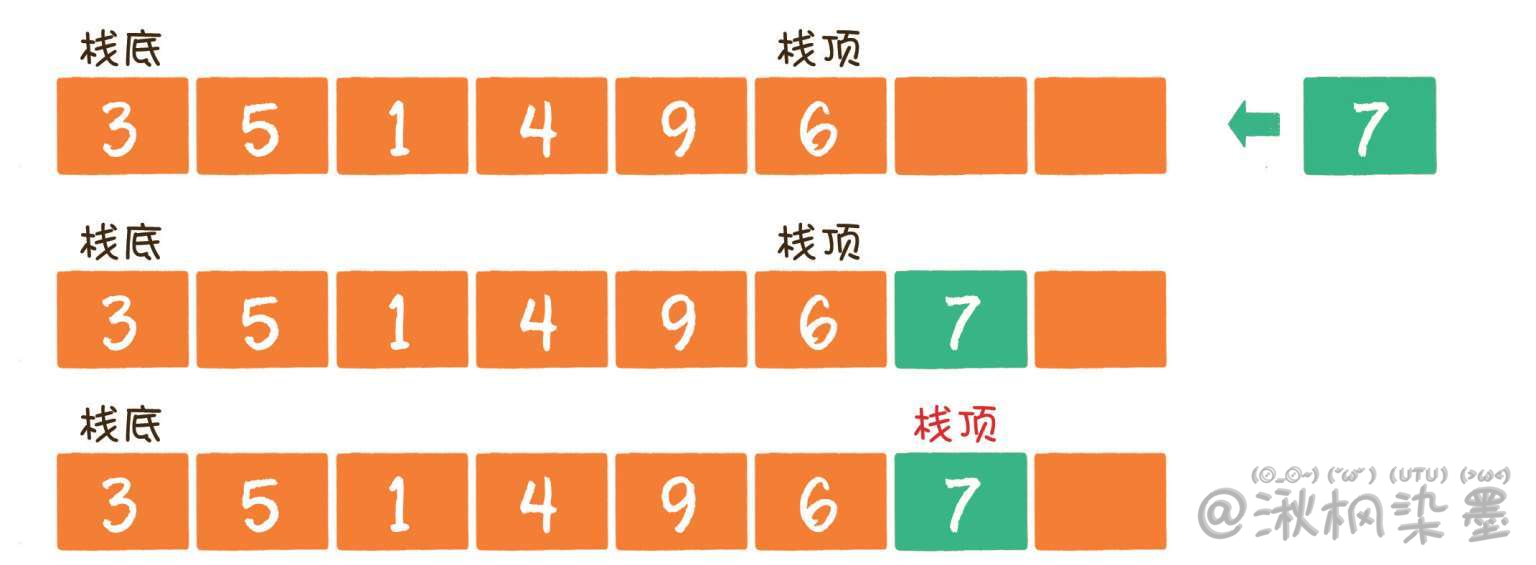
1. 入栈

时间复杂度：O(1)

入栈操作（push）就是把新元素放入栈中，只允许从栈顶一侧放入元素，新元素的位置将会成为新的栈顶。

这里以数组实现为例

2. 出栈

时间复杂度：O(1)

出栈操作（pop）就是把元素从栈中弹出，只有栈顶元素才允许出栈，出栈元素的前一个元素将会成为新的栈顶。

这里以数组实现为例。

完整代码

public class MyStack {

    private int[] array;
    private int maxSize;
    private int top;

    public MyStack(int size) {
        this.maxSize = size;
        array = new int[size];
        top = -1;
    }

    // 压入数据
    public void push(int value) {
        if (top < maxSize - 1) {
            array[++top] = value;
        }
    }

    // 弹出栈顶数据
    public int pop() {
        return array[top--];
    }

    // 访问栈顶数据
    public int peek() {
        return array[top];
    }

    // 判断栈是否为空
    public boolean isEmpty() {
        return top == -1;
    }

    //判断栈是否满了
    public boolean isFull() {
        return top == maxSize - 1;
    }

    public static void main(String[] args) {
        MyStack stack = new MyStack(3);
        stack.push(1);
        stack.push(2);
        stack.push(3);
        System.out.println(stack.peek());           // 3
        while (!stack.isEmpty()) {
            System.out.print(stack.pop() + " ");    // 3 2 1
        }
    }
}

3.3 队列

队列（queue）是一种线性数据结构，队列中的元素只能先入先出（First In First Out，简称FIFO）。队列的出口端叫作队头（front），队列的入口端叫作队尾（rear）。

与栈类似，队列这种数据结构既可以用数组来实现，也可以用链表来实现。

3.4 基本操作

1. 入队

入队（enqueue）就是把新元素放入队列中，只允许在队尾的位置放入元素，新元素的下一个位置将会成为新的队尾。

2. 出队

出队操作（dequeue）就是把元素移出队列，只允许在队头一侧移出元素，出队元素的后一个元素将会成为新的队头。

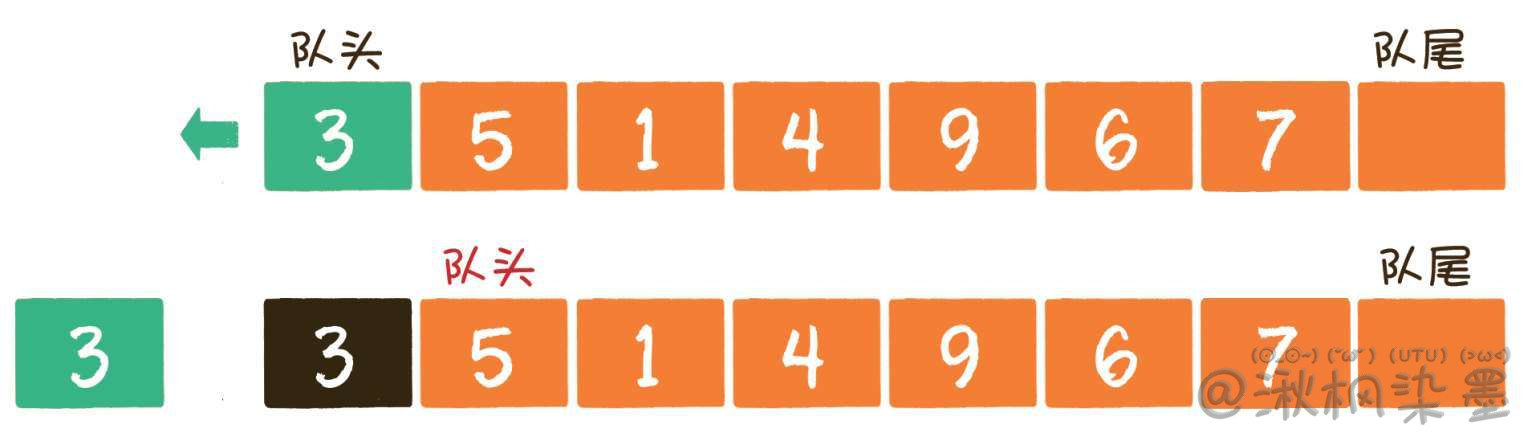
Q：如果用数组实现，不断出队，队头左边的空间失去作用，那队列容量岂不是越来越小了？例如下图：

A：用数组实现的队列可以采用循环队列的方式来维持队列容量的恒定。

循环队列

假设一个队列经过反复的入队和出队操作，还剩下2个元素，在 "物理" 上分布于数组的末尾位置。这时又有一个新元素将要入队。

在数组不做扩容的前提下，如何让新元素入队并确定新的队尾位置呢？可以利用已出队元素留下的空间，让队尾指针重新指回数组的首位。

这样一来，整个队列的元素就 "循环" 起来了。在物理存储上，队尾的位置也可以在队头之前。当再有元素入队时，将其放入数组的首位，队尾指针继续后移即可。

一直到（队尾下标+1）%数组长度 = 队头下标时，代表此队列真的已经满了。需要注意的是，队尾指针指向的位置永远空出1位，所以队列最大容量比数组长度小1。

代码实现

public class MyQueue {

    private int[] array;
    private int front;
    private int rear;

    public MyQueue(int capacity) {
        this.array = new int[capacity];
    }

    /**
     * 入队
     *
     * @param element 入队的元素
     */
    public void enQueue(int element) throws Exception {
        if ((rear + 1) % array.length == front) {
            throw new Exception(" 队列已满！");
        }
        array[rear] = element;
        rear = (rear + 1) % array.length;
    }

    /**
     * 出队
     */
    public int deQueue() throws Exception {
        if (rear == front) {
            throw new Exception(" 队列已空！");
        }
        int deQueueElement = array[front];
        front = (front + 1) % array.length;
        return deQueueElement;
    }

    /**
     * 输出队列
     */
    public void output() {
        for (int i = front; i != rear; i = (i + 1) % array.length) {
            System.out.print(array[i] + " ");
        }
    }

    public static void main(String[] args) throws Exception {
        MyQueue myQueue = new MyQueue(6);
        myQueue.enQueue(3);
        myQueue.enQueue(5);
        myQueue.enQueue(6);
        myQueue.enQueue(8);
        myQueue.enQueue(1);
        myQueue.deQueue();
        myQueue.deQueue();
        myQueue.deQueue();
        myQueue.enQueue(2);
        myQueue.enQueue(4);
        myQueue.enQueue(9);
        myQueue.output();           // 8 1 2 4 9
    }
}

四：散列表

散列表也叫作哈希表(hash table)，这种数据结构提供了键（Key）和值（Value）的映射关系。只要给出一个Key，就可以高效查找到它所匹配的Value，时间复杂度接近于O(1)。

散列表在本质上也是一个数组。通过某种方式，把Key和数组下标进行转换。这个转换的地方叫做哈希函数。

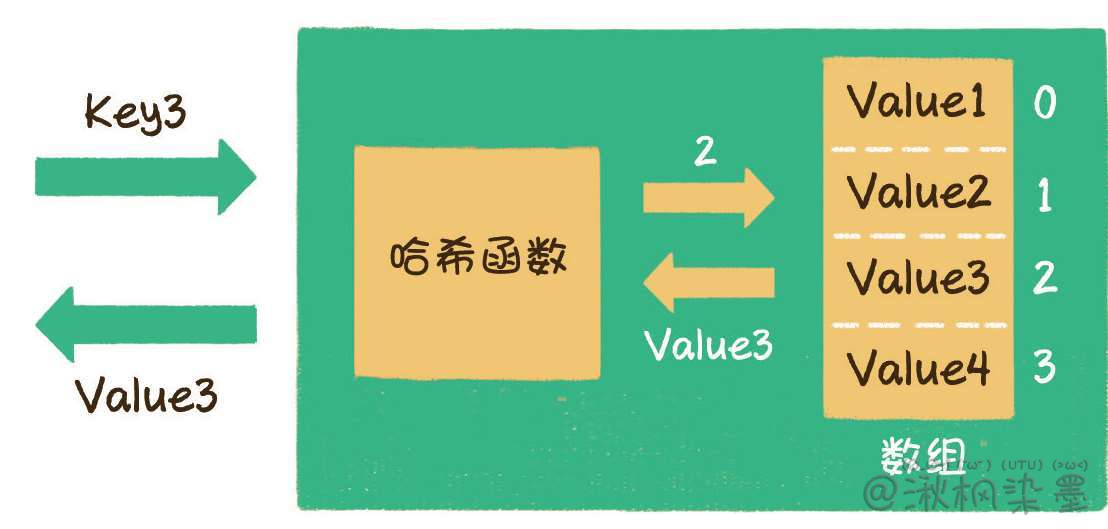
在Java及大多数面向对象的语言中，每一个对象都有属于自己的hashcode，这个hashcode是区分不同对象的重要标识。无论对象自身的类型是什么，它们的hashcode都是一个整型变量。

既然都是整型变量，想要转化成数组的下标也就不难实现了。最简单的转化方式是什么呢？是按照数组长度进行取模运算。

index = HashCode (Key) % Array.length

实际上，JDK（Java Development Kit，Java语言的软件开发工具包）中的哈希函数并没有直接采用取模运算，而是利用了位运算的方式来优化性能。不过在这里可以姑且简单理解成取模操作。

通过哈希函数，可以把字符串或其他类型的Key，转化成数组的下标index。

如给出一个长度为8的数组，则当

key=001121时，

index = HashCode ("001121") % Array.length = 1420036703 % 8 = 7

而当key=this时，

index = HashCode ("this") % Array.length = 3559070 % 8 = 6

4.1 基本操作

1. 写操作(put)

写操作就是在散列表中插入新的键值对(在JDK中叫作Entry)。

如调用hashMap.put("002931", "王五")，意思是插入一组Key为002931、Value为王五的键值对。

具体该怎么做呢？

第1步，通过哈希函数，把Key转化成数组下标5。

第2步，如果数组下标5对应的位置没有元素，就把这个Entry填充到数组下标5的位置。

但是，由于数组的长度是有限的，当插入的Entry越来越多时，不同的Key通过哈希函数获得的下标有可能是相同的。例如002936这个Key对应的数组下标是2；002947这个Key对应的数组下标也是2。

这种情况，就叫作哈希冲突。哈希冲突是无法避免的，既然不能避免，就要想办法来解决。解决哈希冲突的方法主要有两种，一种是开放寻址法，一种是链表法。

开放寻址法的原理很简单，当一个Key通过哈希函数获得对应的数组下标已被占用时，我们可以“另谋高就”，寻找下一个空档位置。

以上面的情况为例，Entry6通过哈希函数得到下标2，该下标在数组中已经有了其他元素，那么就向后移动1位，看看数组下标3的位置是否有空。

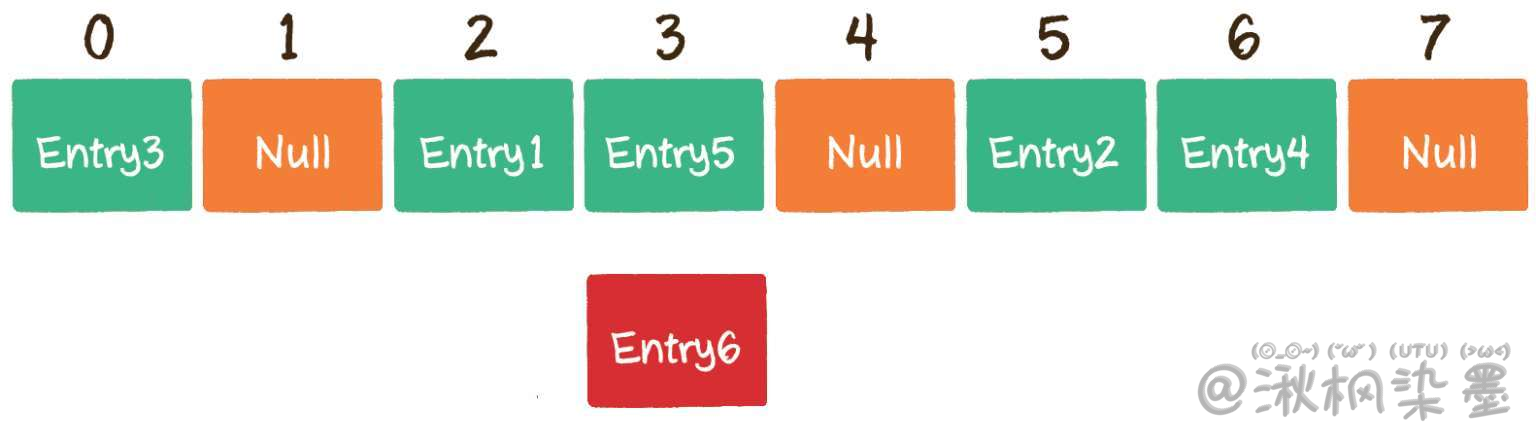
很不巧，下标3也已经被占用，那么就再向后移动1位，看看数组下标4的位置是否有空。

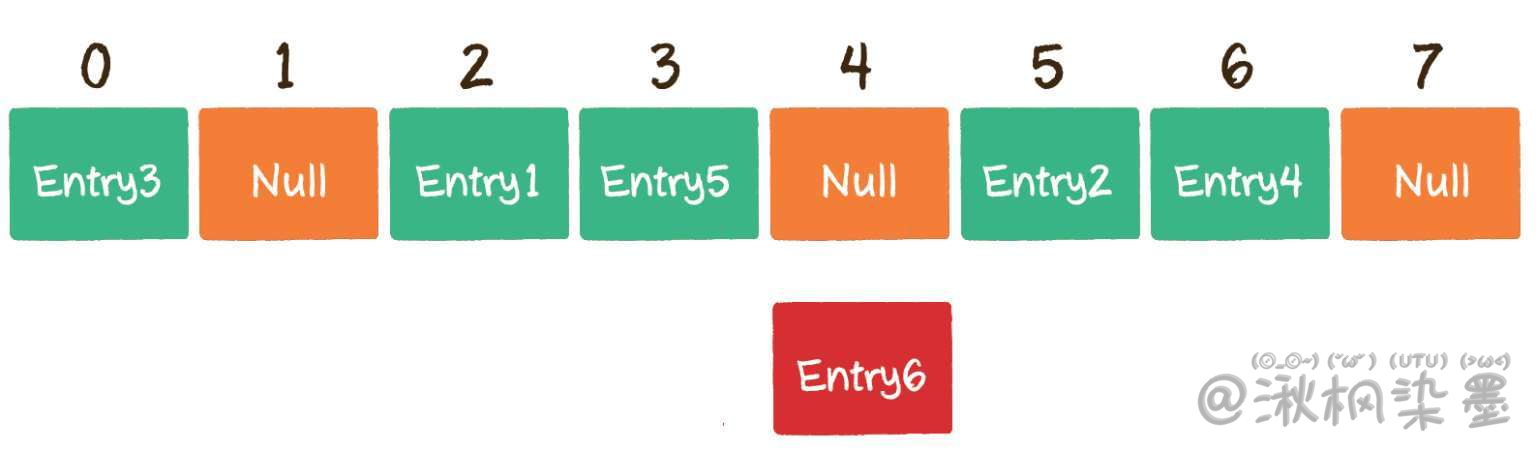
幸运的是，数组下标4的位置还没有被占用，因此把Entry6存入数组下标4的位置。

这就是开放寻址法的基本思路。当然，在遇到哈希冲突时，寻址方式有很多种，并不一定只是简单地寻找当前元素的后一个元素，这里只是举一个简单的示例而已。

在Java中，ThreadLocal所使用的就是开放寻址法。

接下来，重点讲一下解决哈希冲突的另一种方法——链表法。这种方法被应用在了Java的集合类HashMap当中。

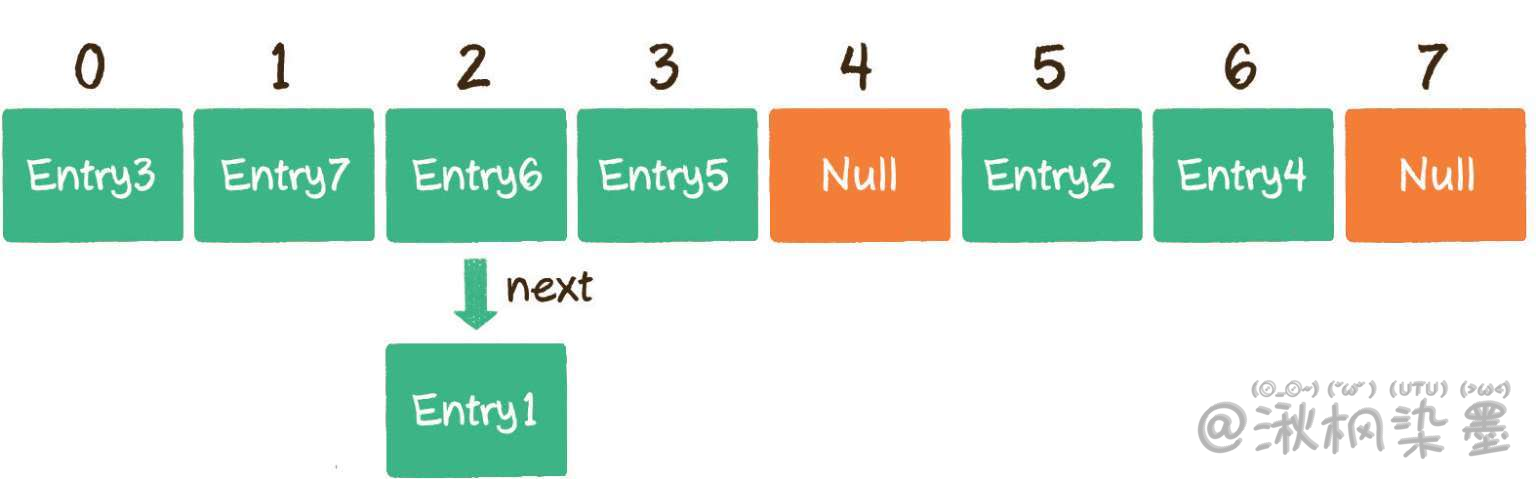
HashMap数组的每一个元素不仅是一个Entry对象，还是一个链表的头节点。每一个Entry对象通过next指针指向它的下一个Entry节点。当新来的Entry映射到与之冲突的数组位置时，只需要插入到对应的链表中即可。

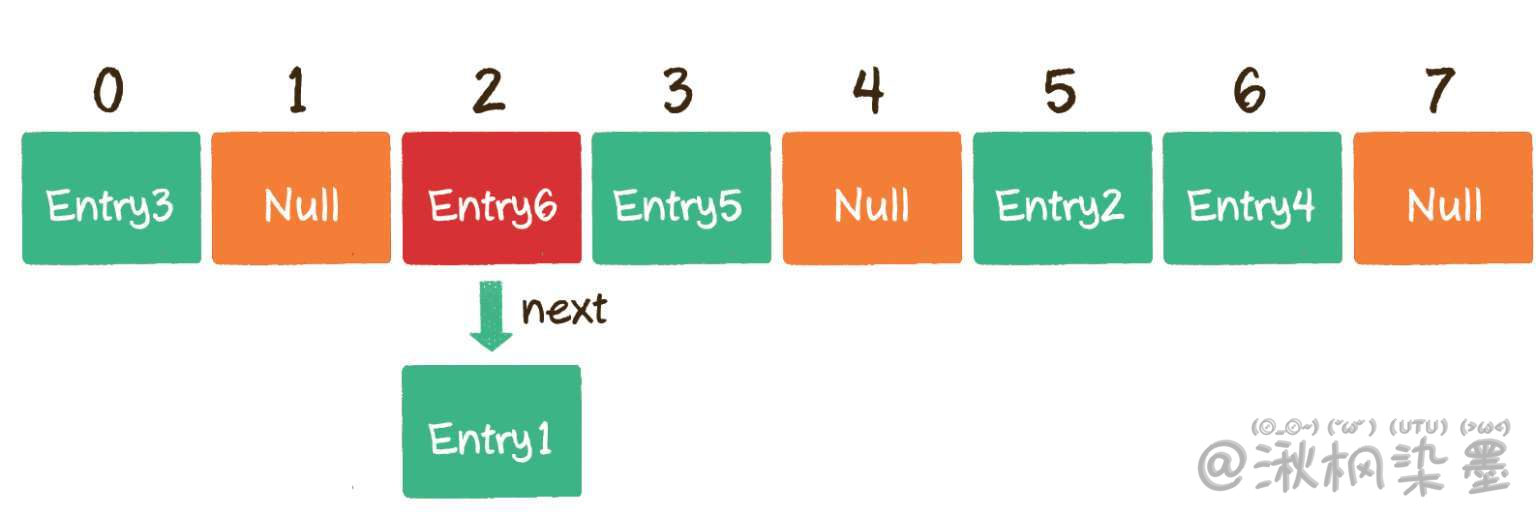
2. 读操作(get)

读操作就是通过给定的Key，在散列表中查找对应的Value。

例如调用 hashMap.get("002936")，意思是查找Key为002936的Entry在散列表中所对应的值。

具体该怎么做呢？下面以链表法为例来讲一下。

第1步，通过哈希函数，把Key转化成数组下标2。

第2步，找到数组下标2所对应的元素，如果这个元素的Key是002936，那么就找到了；如果这个Key不是002936也没关系，由于数组的每个元素都与一个链表对应，我们可以顺着链表慢慢往下找，看看能否找到与Key相匹配的节点。

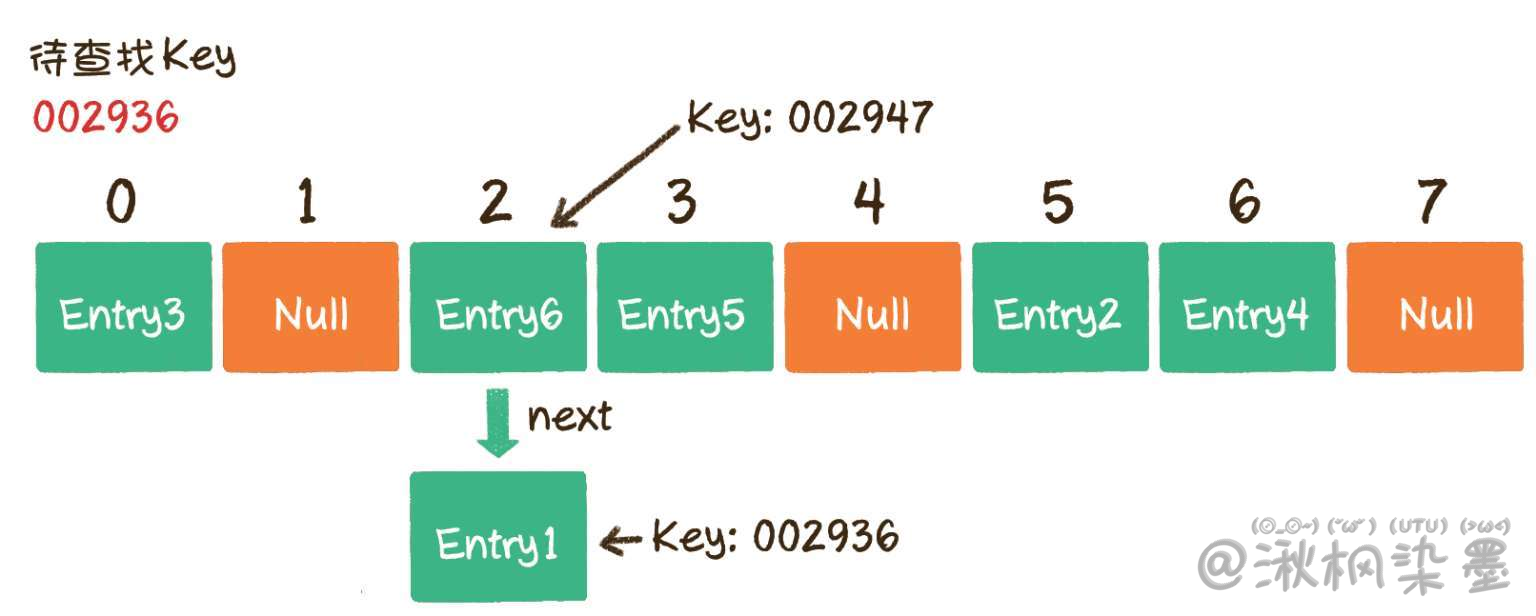
在上图中，首先查到的节点Entry6的Key是002947，和待查找的Key 002936不符。接着定位到链表下一个节点Entry1，发现Entry1的Key 002936正是我们要寻找的，所以返回Entry1的Value即可。

3. 扩容(resize)

首先，什么时候需要进行扩容呢？

当经过多次元素插入，散列表达到一定饱和度时，Key映射位置发生冲突的概率会逐渐提高。这样一来，大量元素拥挤在相同的数组下标位置，形成很长的链表，对后续插入操作和查询操作的性能都有很大影响。

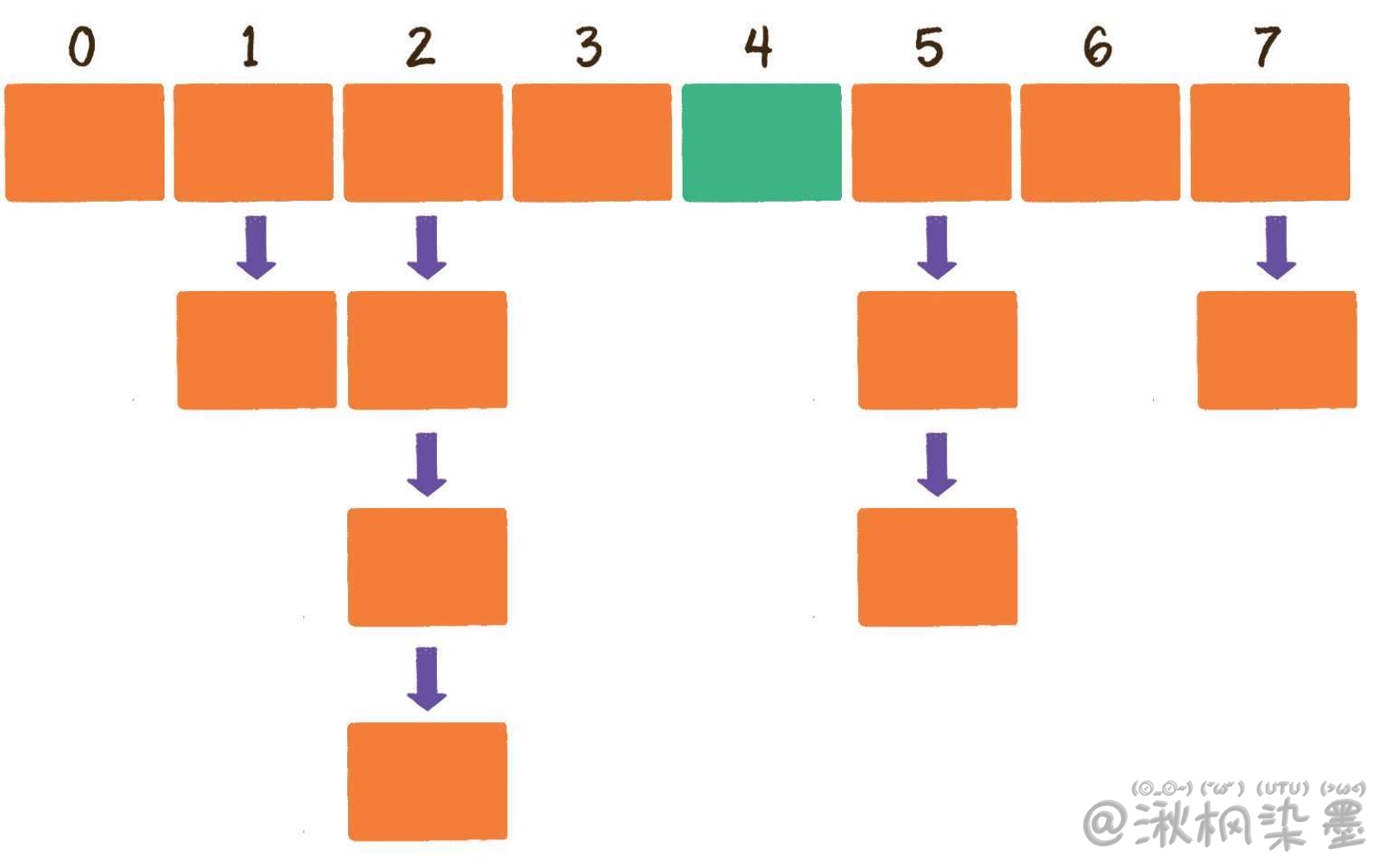
这时，散列表就需要扩展它的长度，也就是进行扩容。

对于JDK中的散列表实现类HashMap来说，影响其扩容的因素有两个。

1. Capacity，即HashMap的当前长度
2. LoadFactor，即HashMap的负载因子，默认值为0.75f

衡量HashMap需要进行扩容的条件如下。

HashMap.Size >= Capacity * LoadFactor

扩容不是简单地把散列表的长度扩大，而是经历了下面两个步骤：

1. 扩容，创建一个新的Entry空数组，长度是原数组的2倍。

2．重新Hash，遍历原Entry数组，把所有的Entry重新Hash到新数组中。为什么要重新Hash呢？因为长度扩大以后，Hash的规则也随之改变。

经过扩容，原本拥挤的散列表重新变得稀疏，原有的Entry也重新得到了尽可能均匀的分配。

扩容前的HashMap。

扩容后的HashMap。

以上就是散列表各种基本操作的原理。

需要注意的是，关于HashMap的实现，JDK 8和以前的版本有着很大的不同。当多个Entry被Hash到同一个数组下标位置时，为了提升插入和查找的效率，HashMap会把Entry的链表转化为红黑树这种数据结构。

五：参考文献

• 《大话数据结构 — 程杰》
• 《漫画算法 — 魏梦舒》