树

摘要

JDK：1.8.0_202

一：前言

树和图就是典型的非线性数据结构。

在数据结构中，树的定义如下：

树（tree）是n（n≥0）个节点的有限集。当n=0时，称为空树。在任意一个非空树中，有如下特点。

1. 有且仅有一个特定的称为根的节点。

2. 当n>1时，其余节点可分为m（m>0）个互不相交的有限集，每一个集合本身又是一个树，并称为根的子树。

下面这张图，就是一个标准的树结构。

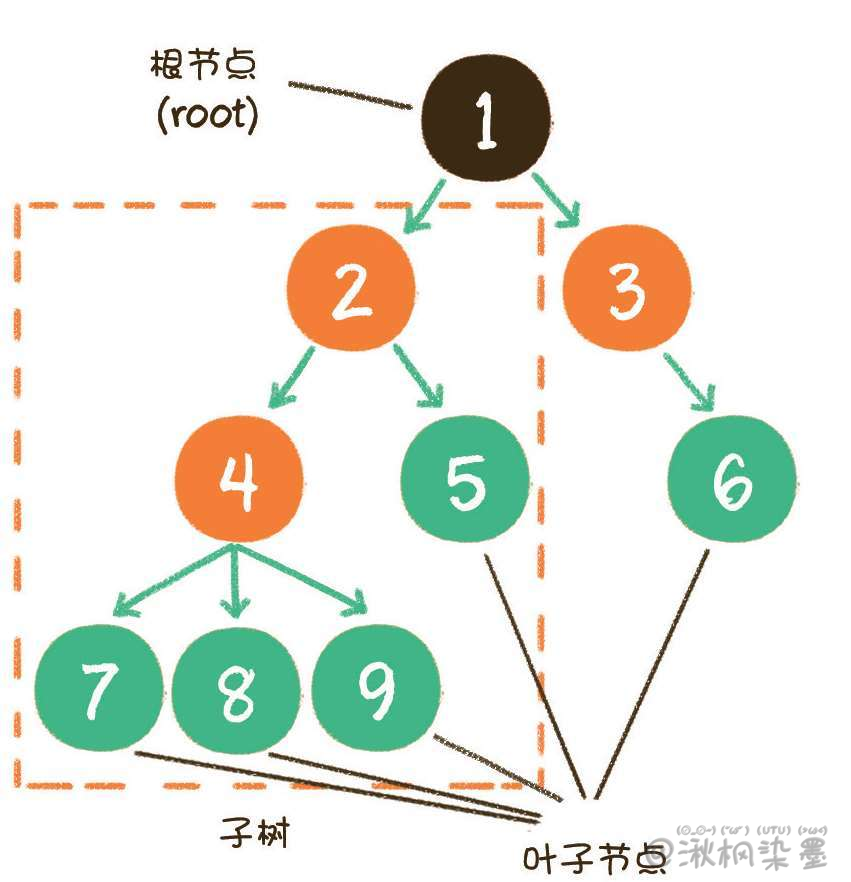
在上图中，节点1是根节点（root）；节点5、6、7、8是树的末端，没有 "孩子"，被称为叶子节点（leaf）。图中的虚线部分，是根节点1的其中一个子树。

同时，树的结构从根节点到叶子节点，分为不同的层级。从一个节点的角度来看，它的上下级和同级节点关系如下。

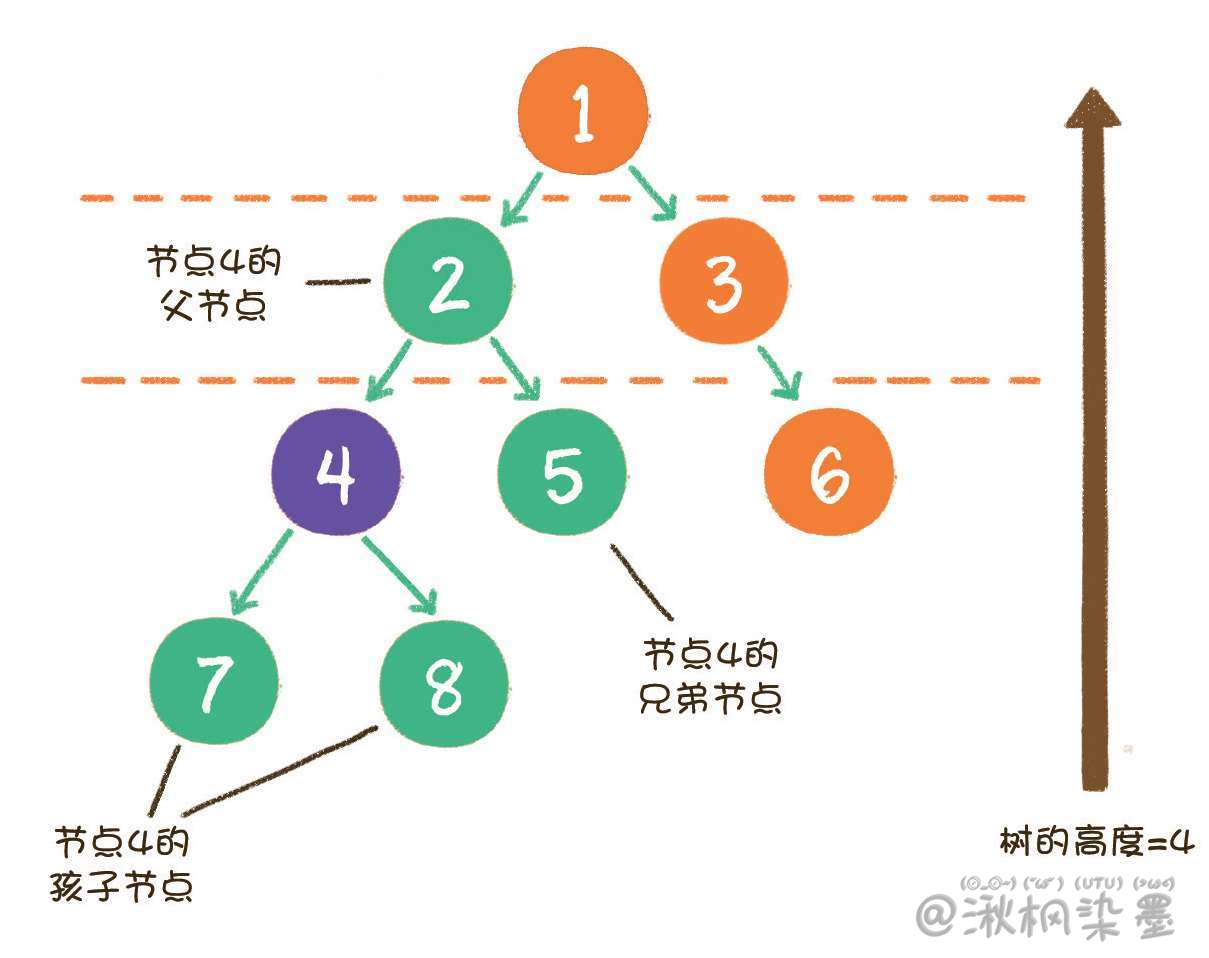
在上图中，节点4的上一级节点，是节点4的父节点（parent）；从节点4衍生出来的节点，是节点4的孩子节点（child）；和节点4同级，由同一个父节点衍生出来的节点，是节点4的兄弟节点（sibling）。树的最大层级数，被称为树的高度或深度。显然，上图这个树的高度是4。

二：二叉树

二叉树（binary tree）是树的一种特殊形式。二叉，顾名思义，这种树的每个节点最多有2个孩子节点。注意，这里是最多有2个，也可能只有1个，或者没有孩子节点。

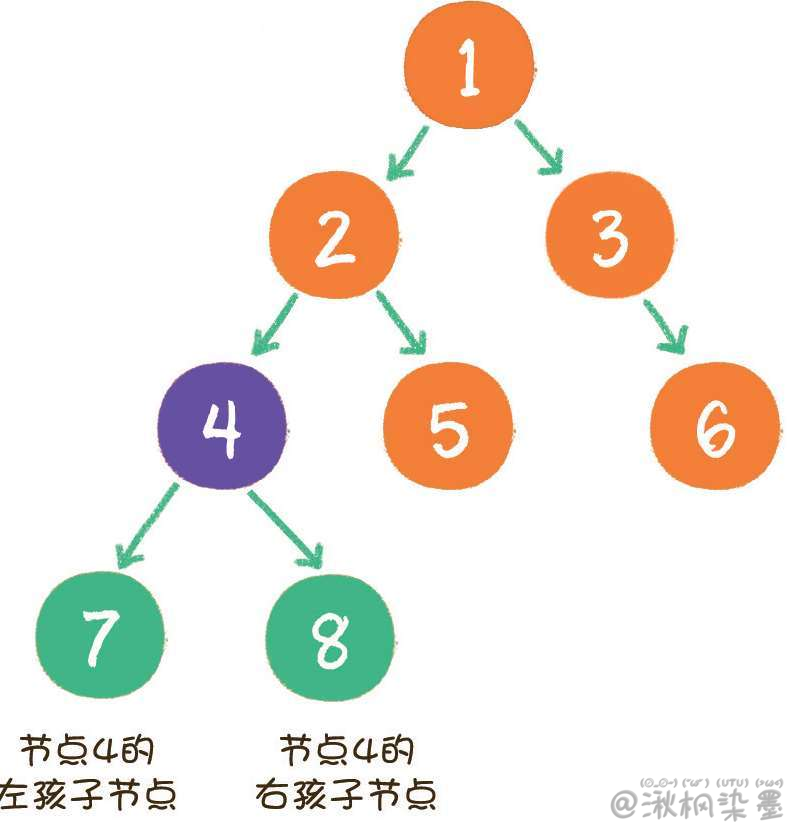
二叉树节点的两个孩子节点，一个被称为左孩子（left child），一个被称为右孩子**（right child）**。这两个孩子节点的顺序是固定的，就像人的左手就是左手，右手就是右手，不能够颠倒或混淆。

此外，二叉树还有两种特殊形式，一个叫作满二叉树，另一个叫作完全二叉树。

2.1 满二叉树

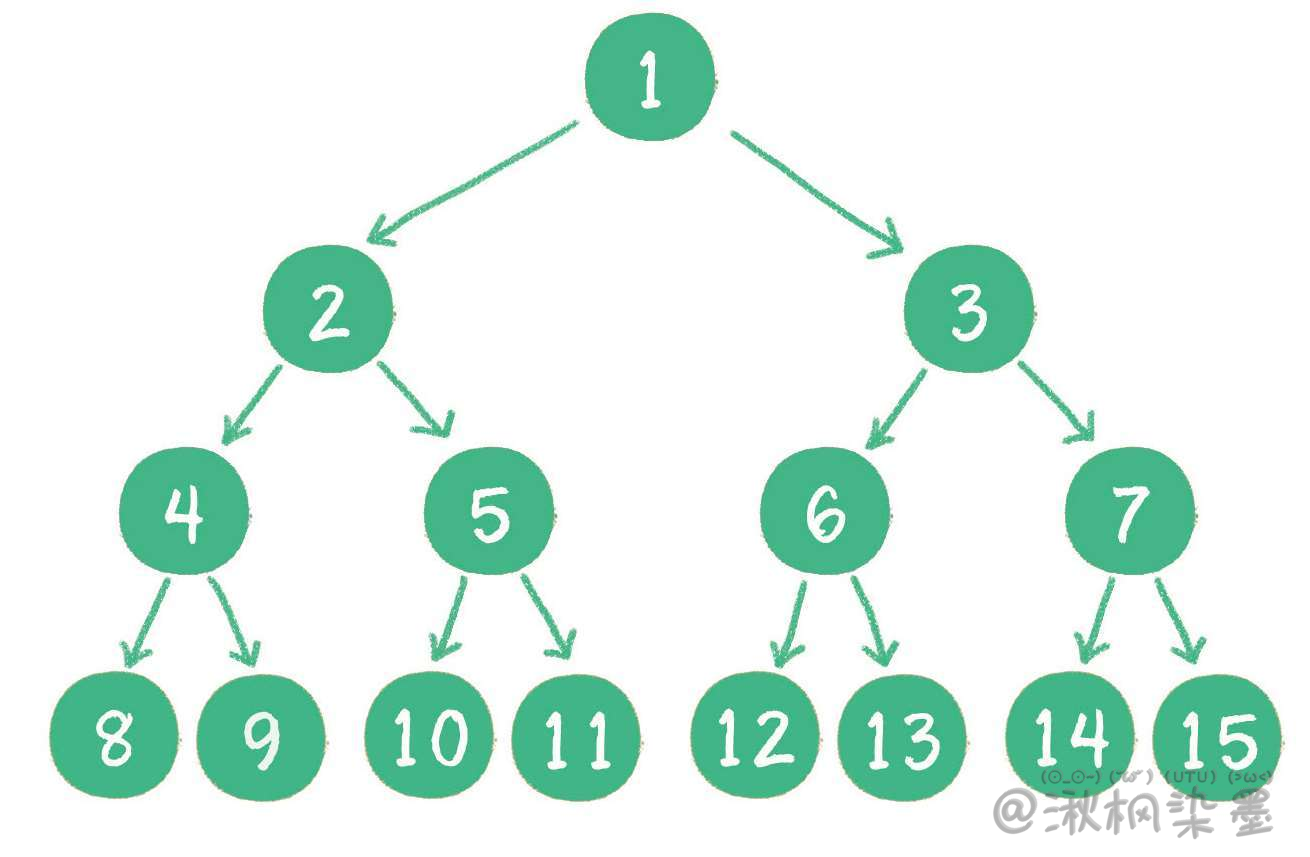
一个二叉树的所有非叶子节点都存在左右孩子，并且所有叶子节点都在同一层级上，那么这个树就是满二叉树。

2.2 完全二叉树

对一个有n个节点的二叉树，按层级顺序编号，则所有节点的编号为从1到n。如果这个树所有节点和同样深度的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完全二叉树。

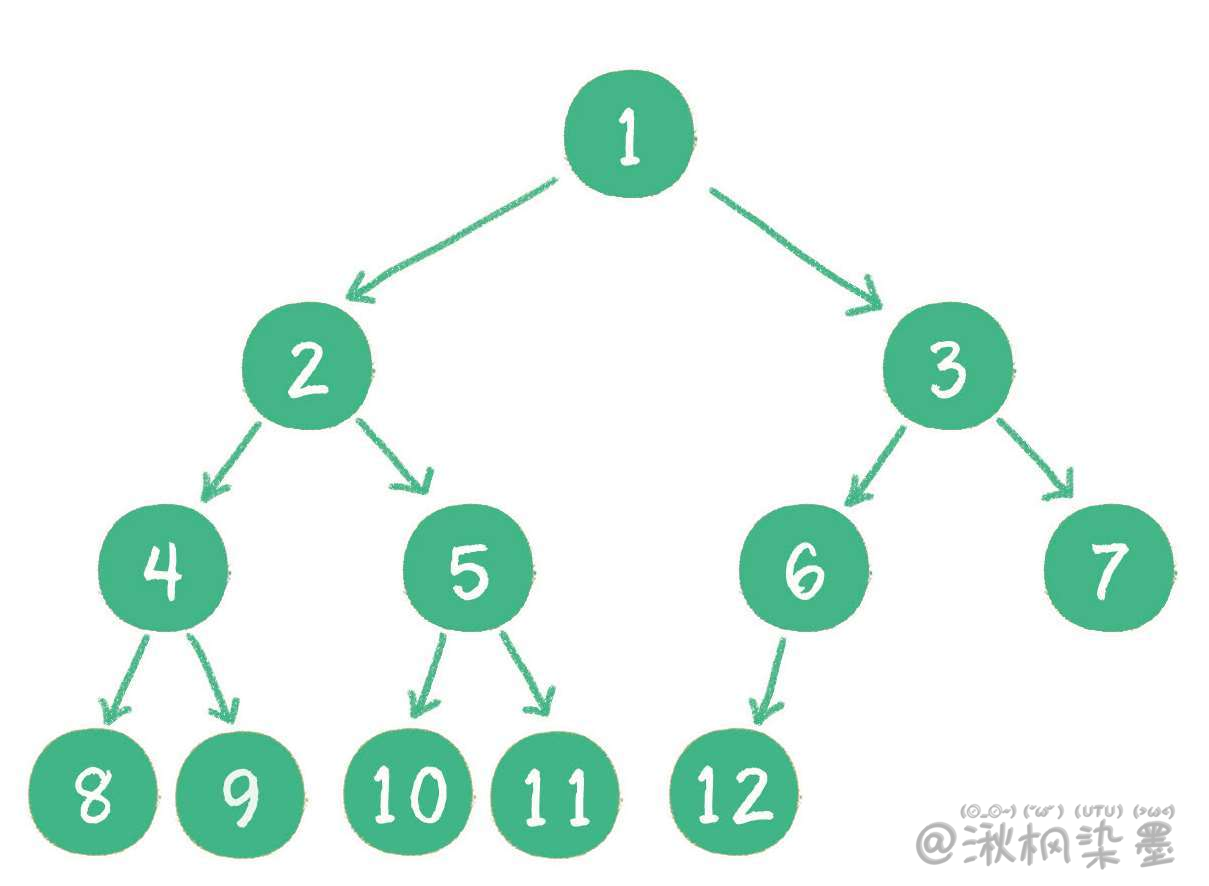
在上图中，二叉树编号从1到12的12个节点，和前面满二叉树编号从1到12的节点位置完全对应。因此这个树是完全二叉树。

完全二叉树的条件没有满二叉树那么苛刻：满二叉树要求所有分支都是满的；而完全二叉树只需保证最后一个节点之前的节点都齐全即可。

2.3 内存存储格式

二叉树属于逻辑结构，可以通过 链式存储结构 和 数组 这物理结构来表达。

1. 链式存储结构

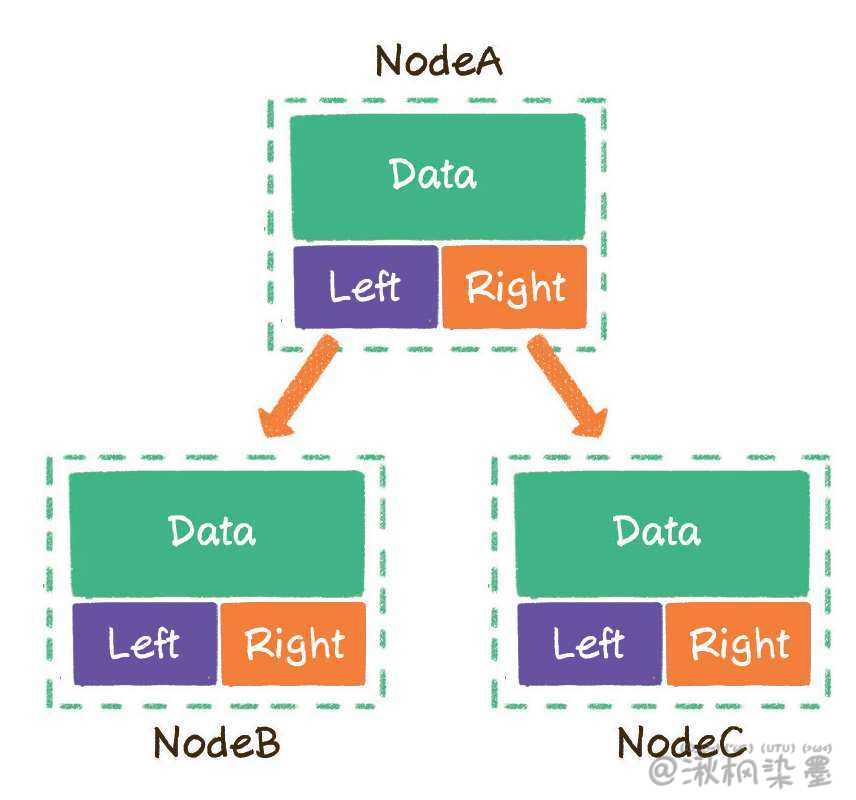
二叉树的每一个节点包含3部分：

• 存储数据的data变量；
• 指向左孩子的left指针；
• 指向右孩子的right指针。

2. 数组

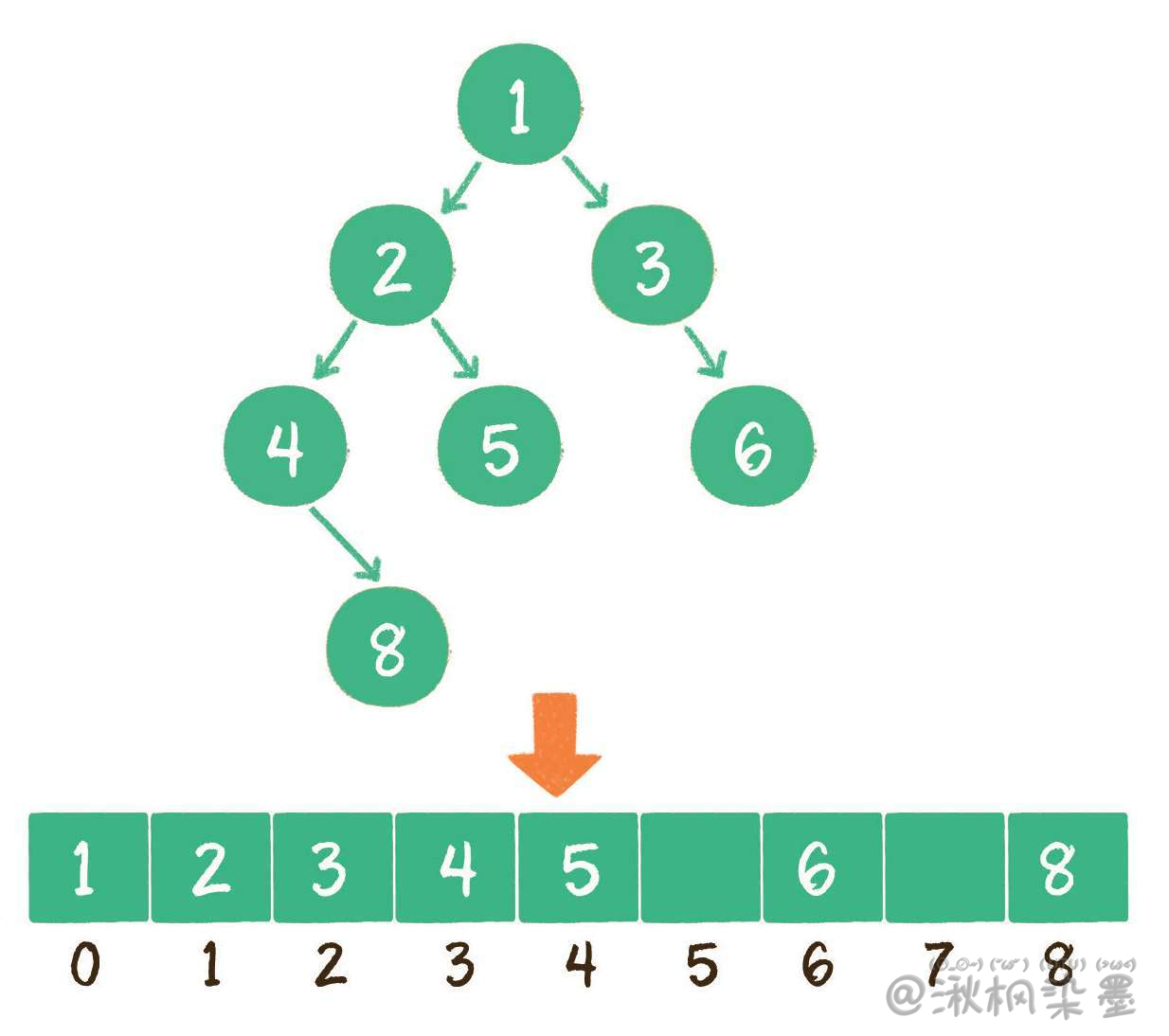
使用数组存储时，会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺，则数组的相应位置也空出来。

为什么这样设计呢？因为这样可以更方便地在数组中定位二叉树的孩子节点和父节点。

假设一个父节点的下标是parent，那么它的左孩子节点下标就是 2×parent + 1；右孩子节点下标就是 2×parent + 2。

反过来，假设一个左孩子节点的下标是leftChild，那么它的父节点下标就是 (leftChild-1)/ 2。

假如节点4在数组中的下标是3，节点4是节点2的左孩子，节点2的下标可以直接通过计算得出 节点2的下标 = (3-1)/2 = 1。

显然，对于一个稀疏的二叉树来说，用数组表示法是非常浪费空间的。

2.4 二叉树的应用

二叉树包含许多特殊的形式，每一种形式都有自己的作用，但是其最主要的应用还在于进行 查找操作 和 维持相对顺序 这两个方面。

1. 查找

二叉查找树(binary search tree)。这种二叉树的主要作用就是进行查找操作。

二叉查找树在二叉树的基础上增加了以下几个条件。

• 如果左子树不为空，则左子树上所有节点的值均小于根节点的值；
• 如果右子树不为空，则右子树上所有节点的值均大于根节点的值；
• 左、右子树也都是二叉查找树。

下图就是一个标准的二叉查找树：

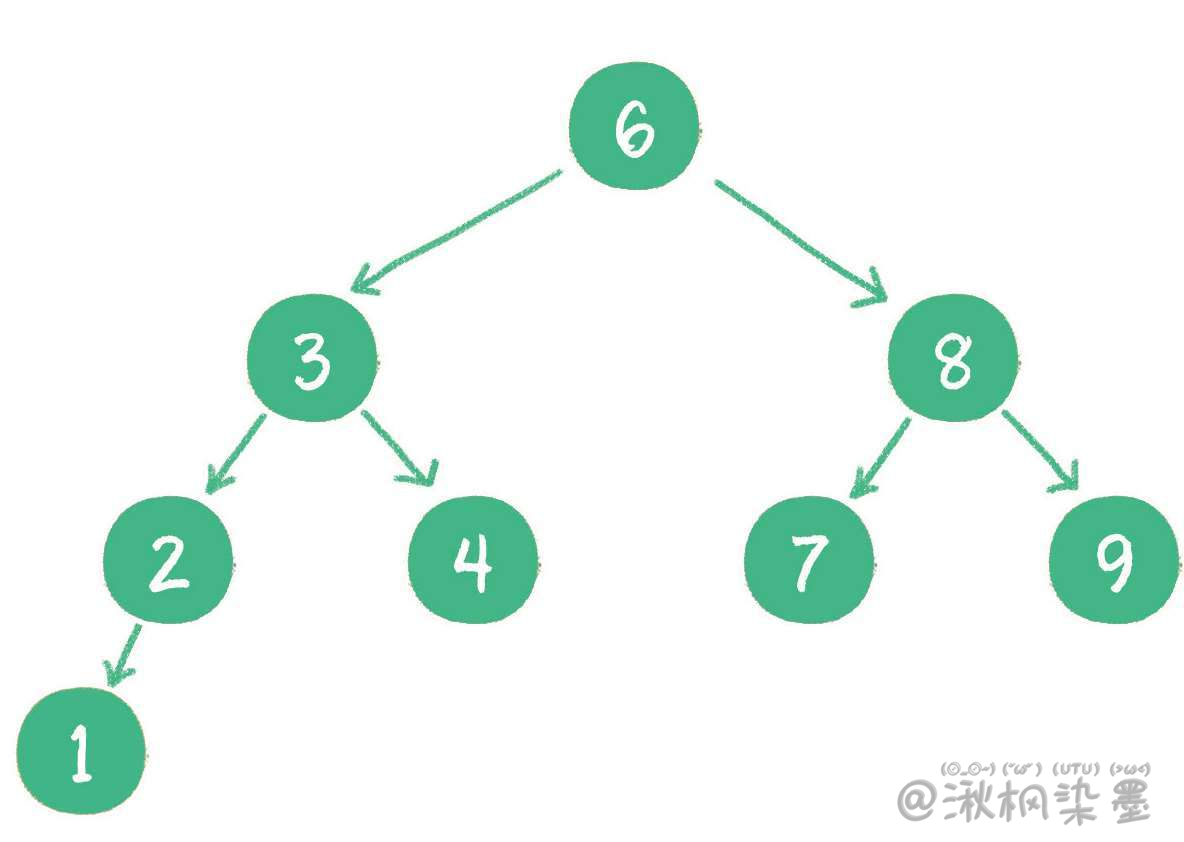
查找值为4的节点，步骤如下：

1. 访问根节点6，发现4<6；
2. 访问节点6的左孩子节点3，发现4>3；
3. 访问节点3的右孩子节点4，发现4=4，这正是要查找的节点。

对于一个节点分布相对均衡的二叉查找树来说，如果节点总数是n，那么搜索节点的时间复杂度就是O(logn)，和树的深度是一样的。

2. 维持相对顺序

二叉查找树要求左子树小于父节点，右子树大于父节点，正是这样保证了二叉树的有序性。

因此二叉查找树还有另一个名字——二叉排序树（binary sort tree）。

新插入的节点，同样要遵循二叉排序树的原则。例如插入新元素5，由于5<6，5>3，5>4，所以5最终会插入到节点4的右孩子位置。

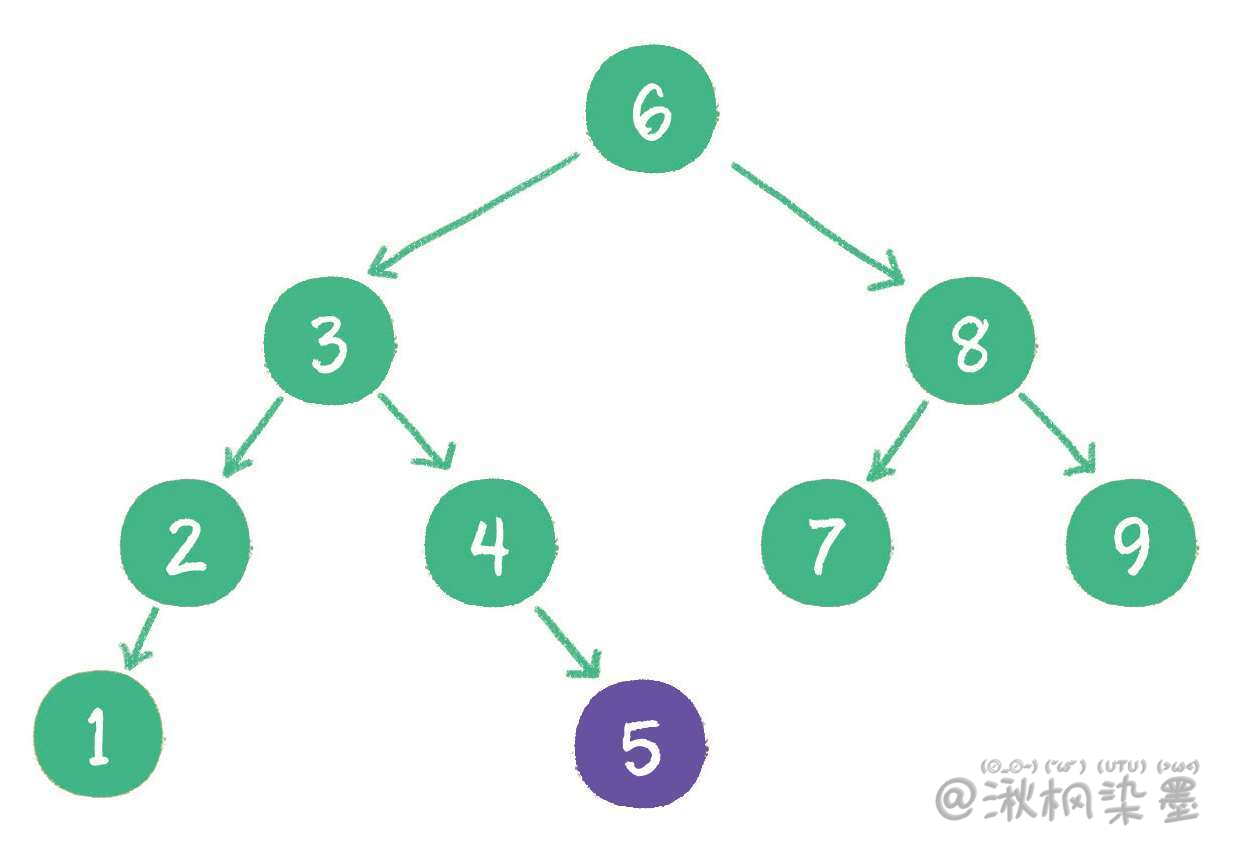
然而却隐藏着一个致命的问题。什么问题呢？下面请试着在二叉查找树中依次插入9、8、7、6、5、4，看看会出现什么结果。

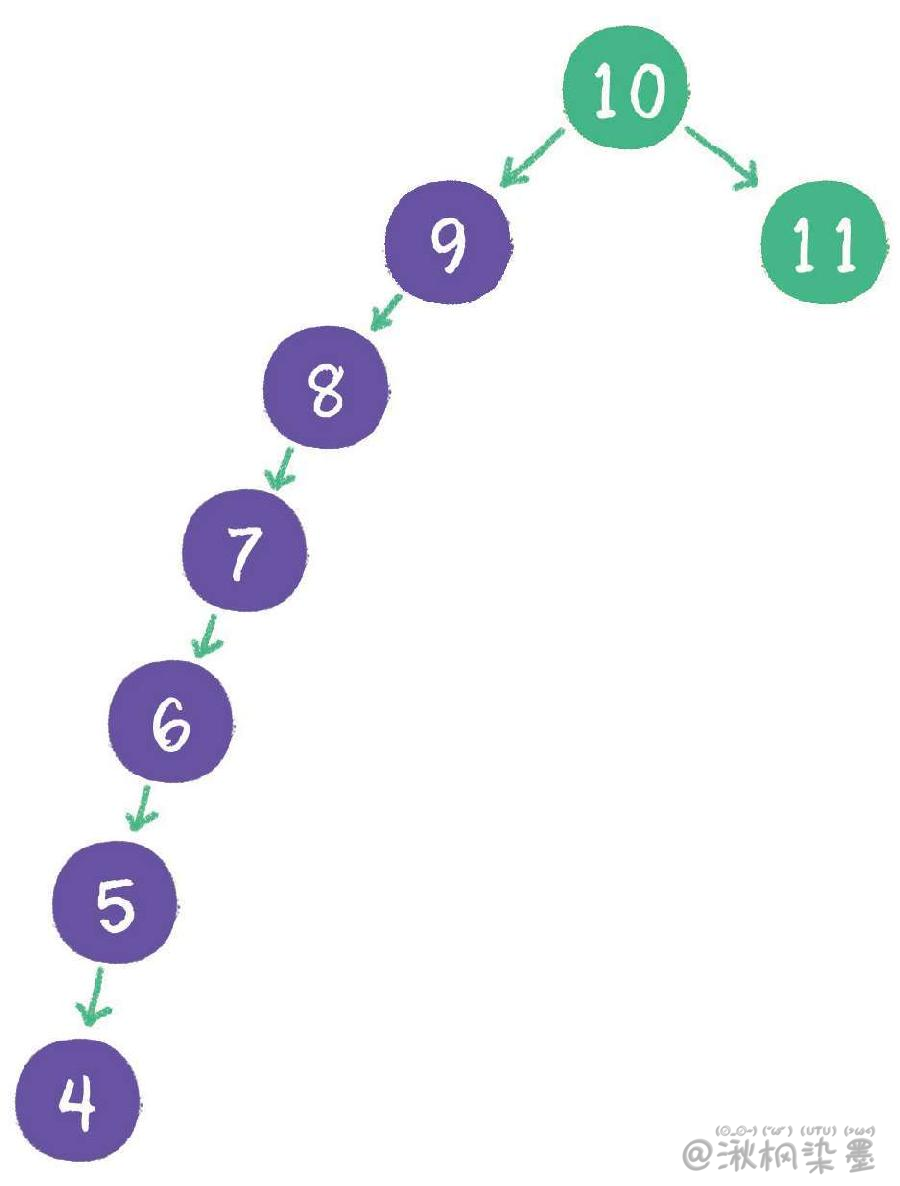
不只是外观看起来变得怪异了，查询节点的时间复杂度也退化成了O(n)。

怎么解决这个问题呢？这就涉及二叉树的自平衡了。二叉树自平衡的方式有多种，如红黑树、AVL树、树堆等。

三：二叉树的遍历

二叉树，是典型的非线性数据结构，遍历时需要把非线性关联的节点转化成一个线性的序列，以不同的方式来遍历，遍历出的序列顺序也不同。

二叉树几种遍历方式：

• 从节点之间位置关系的角度来看，二叉树的遍历分为4种：
  1. 前序遍历
  2. 中序遍历
  3. 后序遍历
  4. 层序遍历
• 从更宏观的角度来看，二叉树的遍历归结为两大类：
  1. 深度优先遍历（前序遍历、中序遍历、后序遍历）
  2. 广度优先遍历（层序遍历）

3.1 深度优先遍历

深度优先和广度优先这两个概念不止局限于二叉树，它们更是一种抽象的算法思想，决定了访问某些复杂数据结构的顺序。在访问树、图，或其他一些复杂数据结构时，这两个概念常常被使用到。

所谓深度优先，顾名思义，就是偏向于纵深，"一头扎到底" 的访问方式。

1. 前序遍历

二叉树的前序遍历，输出顺序是根节点、左子树、右子树。

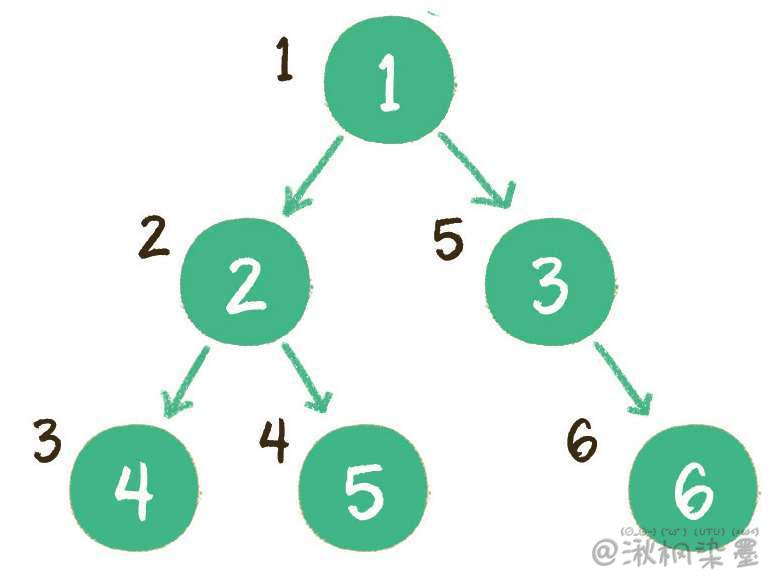
上图就是一个二叉树的前序遍历，每个节点左侧的序号代表该节点的输出顺序，详细步骤如下：

1. 首先输出的是根节点1；
2. 由于根节点1存在左孩子，输出左孩子节点2；
3. 由于节点2也存在左孩子，输出左孩子节点4；
4. 节点4既没有左孩子，也没有右孩子，那么回到节点2，输出节点2的右孩子节点5；
5. 节点5既没有左孩子，也没有右孩子，那么回到节点1，输出节点1的右孩子节点3；
6. 节点3没有左孩子，但是有右孩子，因此输出节点3的右孩子节点6。

2. 中序遍历

二叉树的中序遍历，输出顺序是左子树、根节点、右子树。

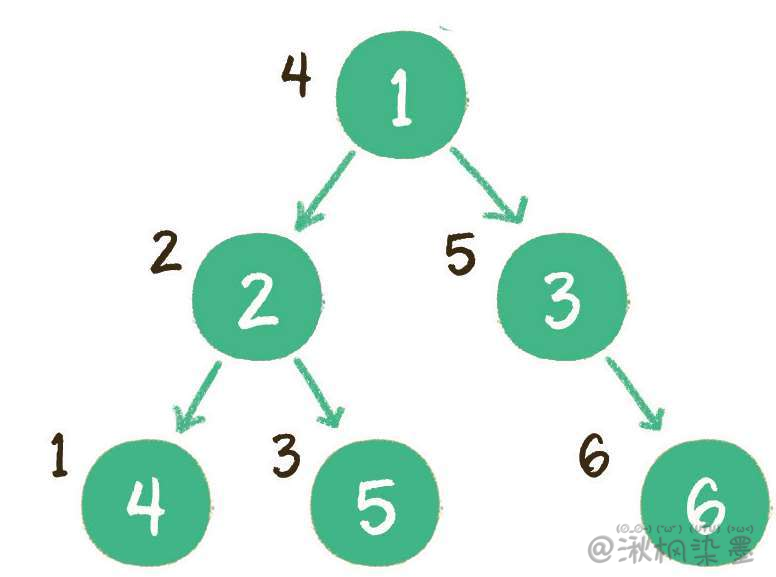
上图就是一个二叉树的中序遍历，每个节点左侧的序号代表该节点的输出顺序，详细步骤如下：

1. 首先访问根节点的左孩子，如果这个左孩子还拥有左孩子，则继续深入访问下去，一直找到不再有左孩子的节点，并输出该节点。显然，第一个没有左孩子的节点是节点4；
2. 依照中序遍历的次序，接下来输出节点4的父节点2；
3. 再输出节点2的右孩子节点5；
4. 以节点2为根的左子树已经输出完毕，这时再输出整个二叉树的根节点1；
5. 由于节点3没有左孩子，所以直接输出根节点1的右孩子节点3；
6. 最后输出节点3的右孩子节点6。

3. 后序遍历

二叉树的后序遍历，输出顺序是左子树、右子树、根节点。

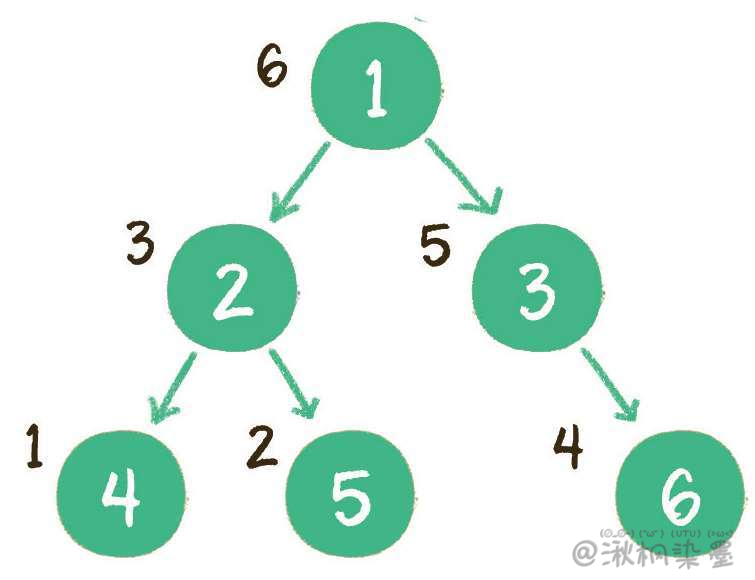
上图就是一个二叉树的后序遍历，每个节点左侧的序号代表该节点的输出顺序。

代码实现

public class DepthForeach {

    /**
     * 构建二叉树
     *
     * @param inputList 输入序列
     */
    public static TreeNode createBinaryTree(LinkedList<Integer> inputList) {
        TreeNode node = null;
        if (inputList == null || inputList.isEmpty()) {
            return null;
        }
        Integer data = inputList.removeFirst();
        if (data != null) {
            node = new TreeNode(data);
            node.leftChild = createBinaryTree(inputList);
            node.rightChild = createBinaryTree(inputList);
        }
        return node;
    }

    /**
     * 二叉树前序遍历
     *
     * @param node 二叉树节点
     */
    public static void preOrderTraveral(TreeNode node) {
        if (node == null) {
            return;
        }
        System.out.print(node.data + " ");
        preOrderTraveral(node.leftChild);
        preOrderTraveral(node.rightChild);
    }

    /**
     * 二叉树中序遍历
     *
     * @param node 二叉树节点
     */
    public static void inOrderTraveral(TreeNode node) {
        if (node == null) {
            return;
        }
        inOrderTraveral(node.leftChild);
        System.out.print(node.data + " ");
        inOrderTraveral(node.rightChild);
    }


    /**
     * 二叉树后序遍历
     *
     * @param node 二叉树节点
     */
    public static void postOrderTraveral(TreeNode node) {
        if (node == null) {
            return;
        }
        postOrderTraveral(node.leftChild);
        postOrderTraveral(node.rightChild);
        System.out.print(node.data + " ");
    }


    /**
     * 二叉树节点
     */
    private static class TreeNode {
        int data;
        TreeNode leftChild;
        TreeNode rightChild;

        TreeNode(int data) {
            this.data = data;
        }
    }

    public static void main(String[] args) {
        LinkedList<Integer> inputList = new LinkedList<>(Arrays.asList(3, 2, 9, null, null, 10, null,
                null, 8, null, 4));
        TreeNode treeNode = createBinaryTree(inputList);
        System.out.print("前序遍历：");
        preOrderTraveral(treeNode);     // 3 2 9 10 8 4
        System.out.println();
        System.out.print("中序遍历：");
        inOrderTraveral(treeNode);      // 9 2 10 3 8 4
        System.out.println();
        System.out.print("后序遍历：");
        postOrderTraveral(treeNode);    // 9 10 2 4 8 3
    }

}

代码中值得注意的一点是二叉树的构建。二叉树的构建方法有很多，这里把一个线性的链表转化成非线性的二叉树，链表节点的顺序恰恰是二叉树前序遍历的顺序。链表中的空值，代表二叉树节点的左孩子或右孩子为空的情况。

在代码的main函数中，通过 {3,2,9,null,null,10,null,null,8,null,4} 这样一个线性序列，构建成的二叉树如下。

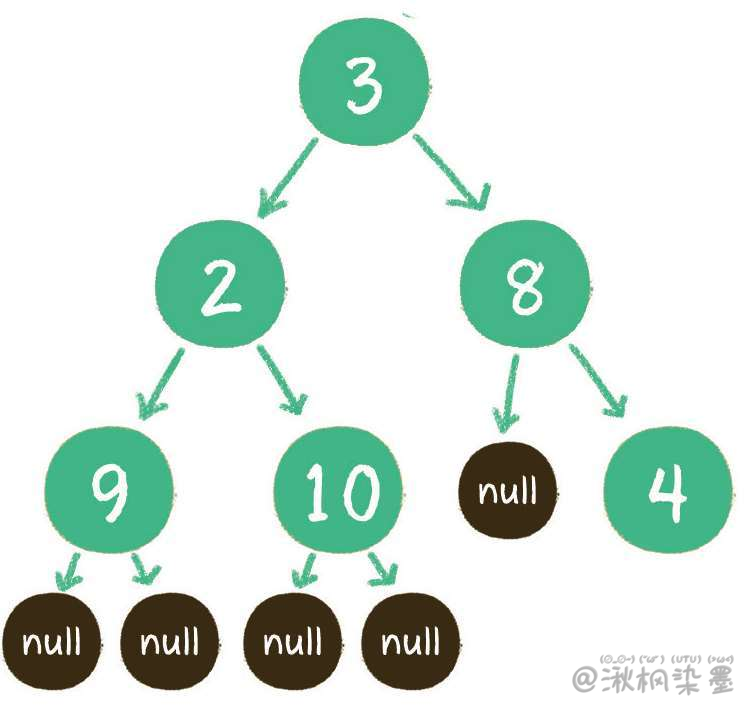
3.2 广度优先遍历

如果说深度优先遍历是在一个方向上 "一头扎到底"，那么广度优先遍历则恰恰相反：先在各个方向上各走出1步，再在各个方向上走出第2步、第3步……一直到各个方向全部走完。

层序遍历，顾名思义，就是二叉树按照从根节点到叶子节点的层次关系，一层一层横向遍历各个节点。

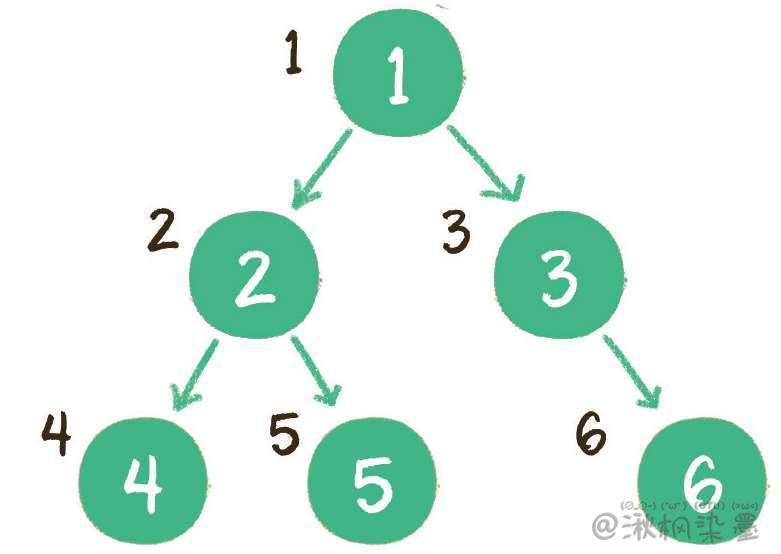
上图就是一个二叉树的层序遍历，每个节点左侧的序号代表该节点的输出顺序。

可是，二叉树同一层次的节点之间是没有直接关联的，如何实现这种层序遍历呢？这里同样需要借助一个数据结构来辅助工作，这个数据结构就是队列。

详细遍历步骤如下：

1. 根节点1进入队列；
2. 节点1出队，输出节点1，并得到节点1的左孩子节点2、右孩子节点3。让节点2和节点3入队；
3. 节点2出队，输出节点2，并得到节点2的左孩子节点4、右孩子节点5。让节点4和节点5入队；
4. 节点3出队，输出节点3，并得到节点3的右孩子节点6。让节点6入队；
5. 节点4出队，输出节点4，由于节点4没有孩子节点，所以没有新节点入队；
6. 节点5出队，输出节点5，由于节点5同样没有孩子节点，所以没有新节点入队；
7. 节点6出队，输出节点6，节点6没有孩子节点，没有新节点入队。

代码实现

/**
 * 二叉树层序遍历
 * @param root   二叉树根节点
 */
public static void levelOrderTraversal(TreeNode root){
	Queue<TreeNode> queue = new LinkedList<TreeNode>();
    queue.offer(root);
    while(!queue.isEmpty()){
        TreeNode node = queue.poll();
        System.out.println(node.data);
        if(node.leftChild != null){
        	queue.offer(node.leftChild);
        }
        if(node.rightChild != null){
        	queue.offer(node.rightChild);
        }
    }
}

四：二叉堆

二叉堆本质上是一种完全二叉树，它分为两个类型。二叉堆的根节点叫作堆顶。

1. 最大堆；
2. 最小堆。

什么是最大堆呢？最大堆的任何一个父节点的值，都大于或等于它左、右孩子节点的值。

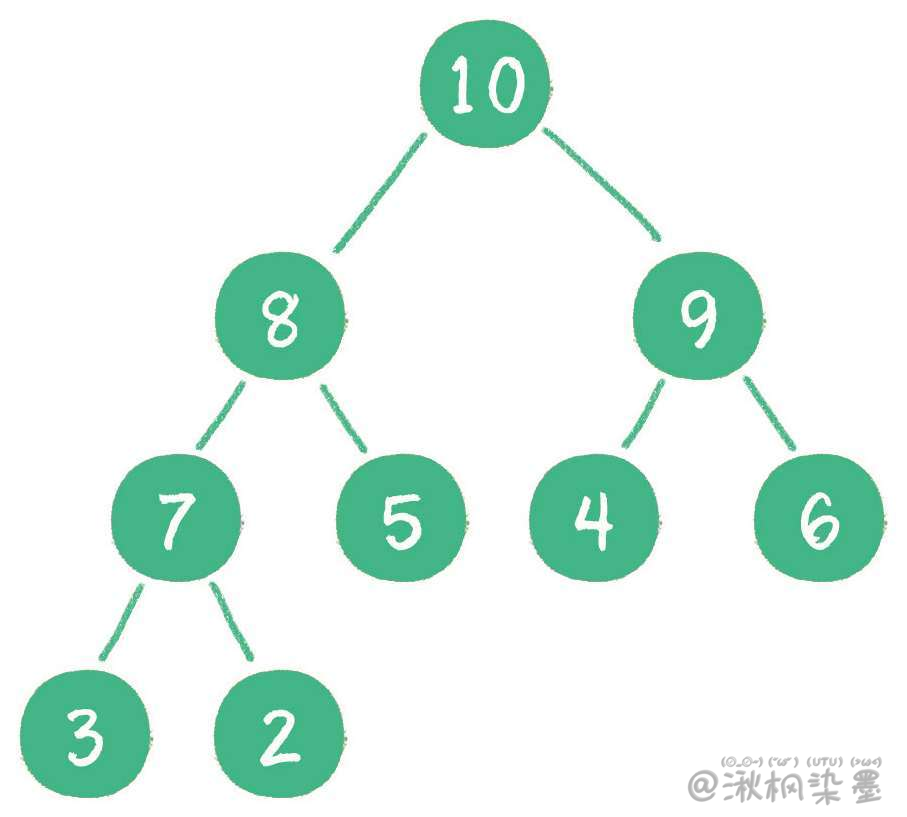
什么是最小堆呢？最小堆的任何一个父节点的值，都小于或等于它左、右孩子节点的值。

如何构建一个堆呢？这就需要依靠二叉堆的自我调整了。

4.1 二叉堆的自我调整

对于二叉堆，有如下几种操作：

1. 插入节点；
2. 删除节点；
3. 构建二叉堆。

这几种操作都基于堆的自我调整。所谓堆的自我调整，就是把一个不符合堆性质的完全二叉树，调整成一个堆。

下面以最小堆为例：

4.2 插入节点

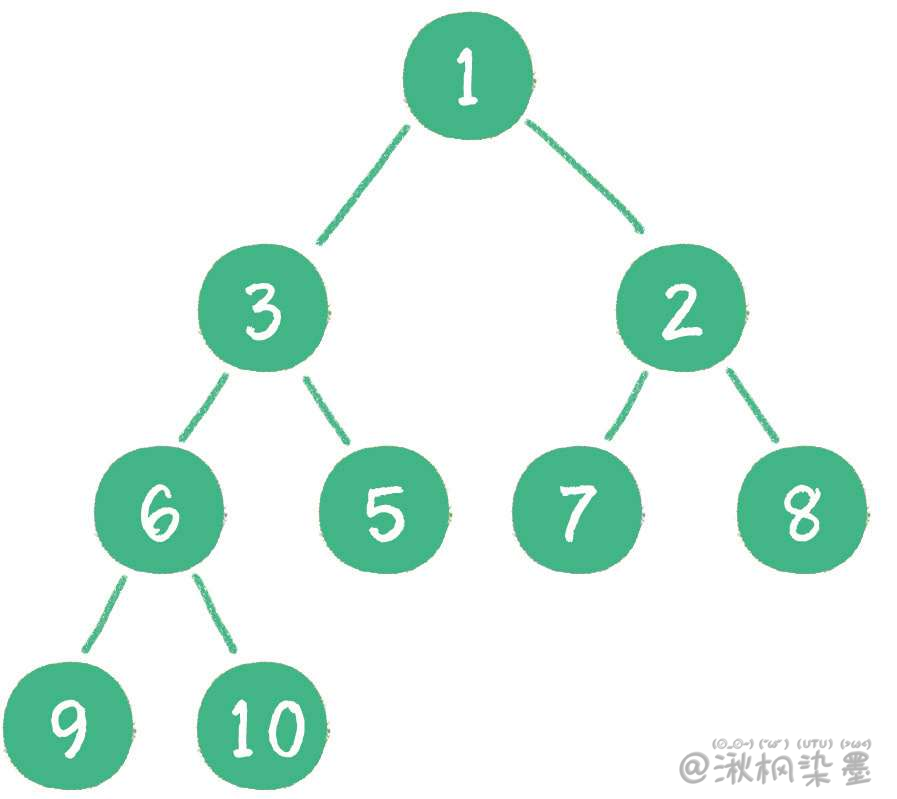
当二叉堆插入节点时，插入位置是完全二叉树的最后一个位置。例如插入一个新节点，值是 0。

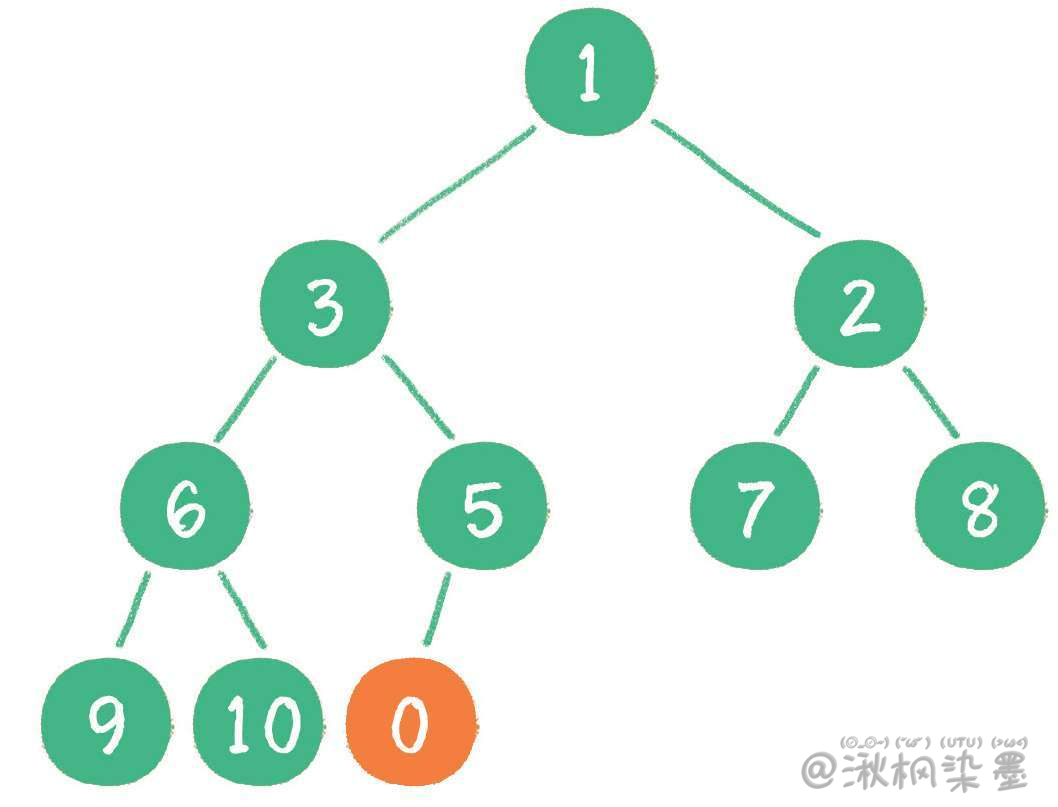
这时，新节点的父节点5比0大，显然不符合最小堆的性质。于是让新节点 "上浮"，和父节点交换位置。

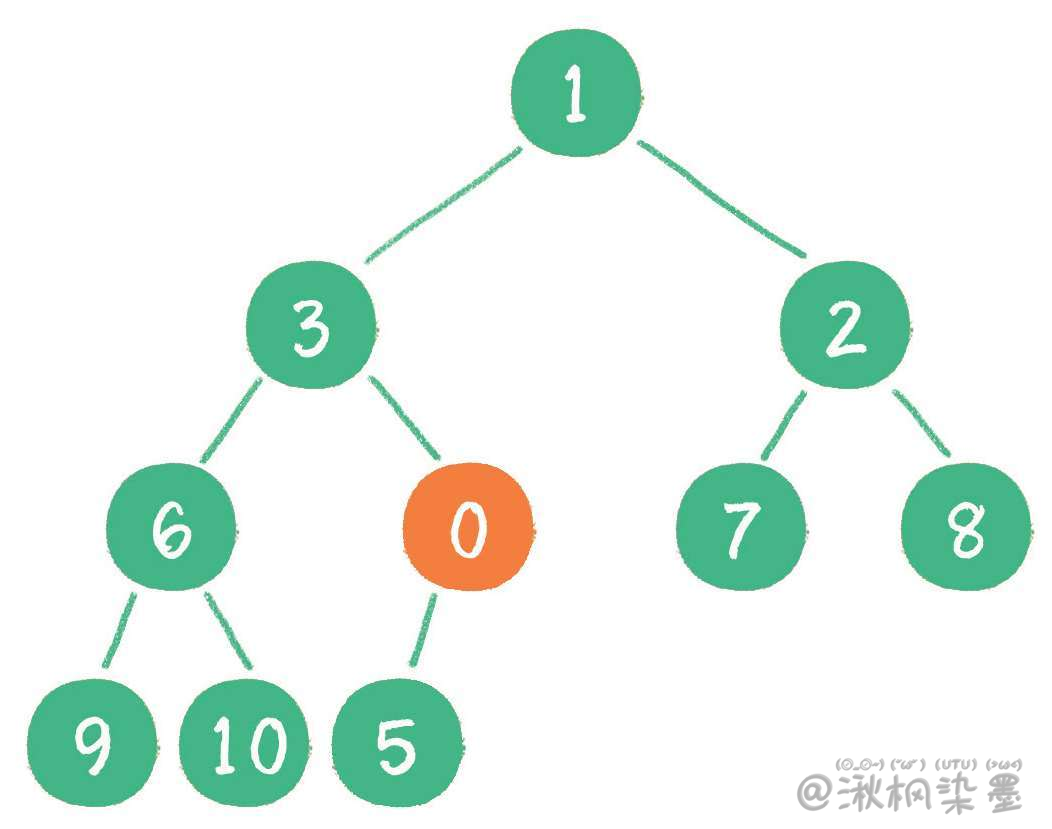
继续用节点0和父节点3做比较，因为0小于3，则让新节点继续 "上浮"。

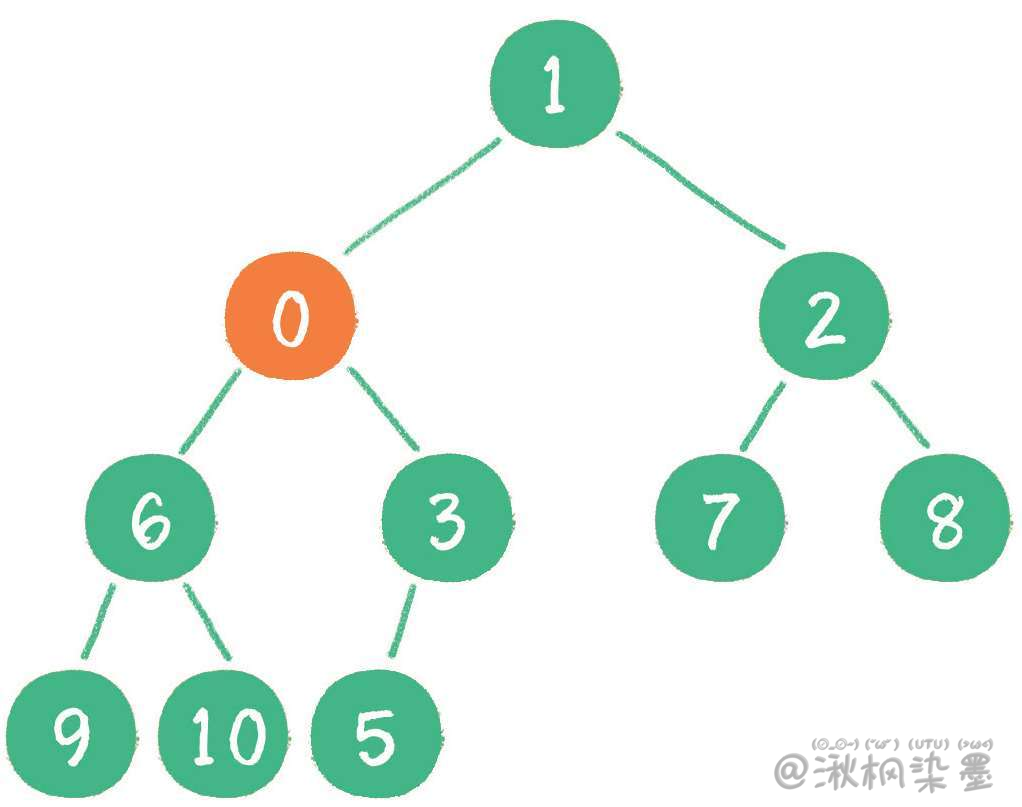
继续比较，最终新节点0 "上浮" 到了堆顶位置。

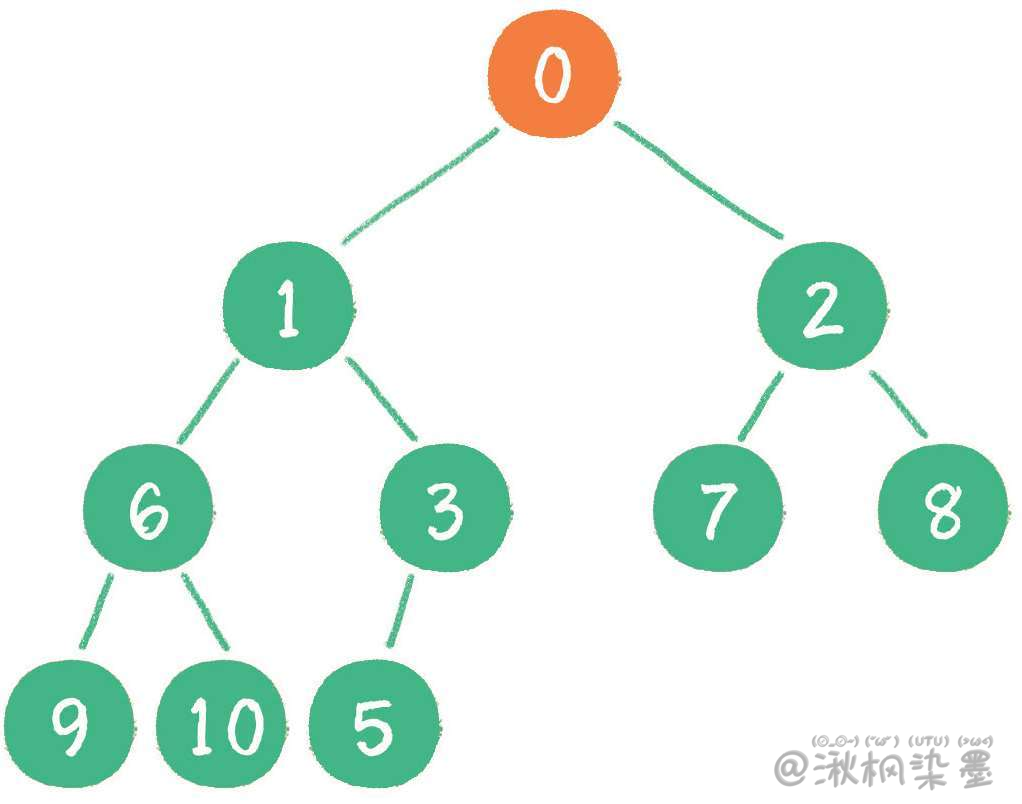
4.3 删除节点

二叉堆删除节点的过程和插入节点的过程正好相反，所删除的是处于堆顶的节点。例如删除最小堆的堆顶节点1。

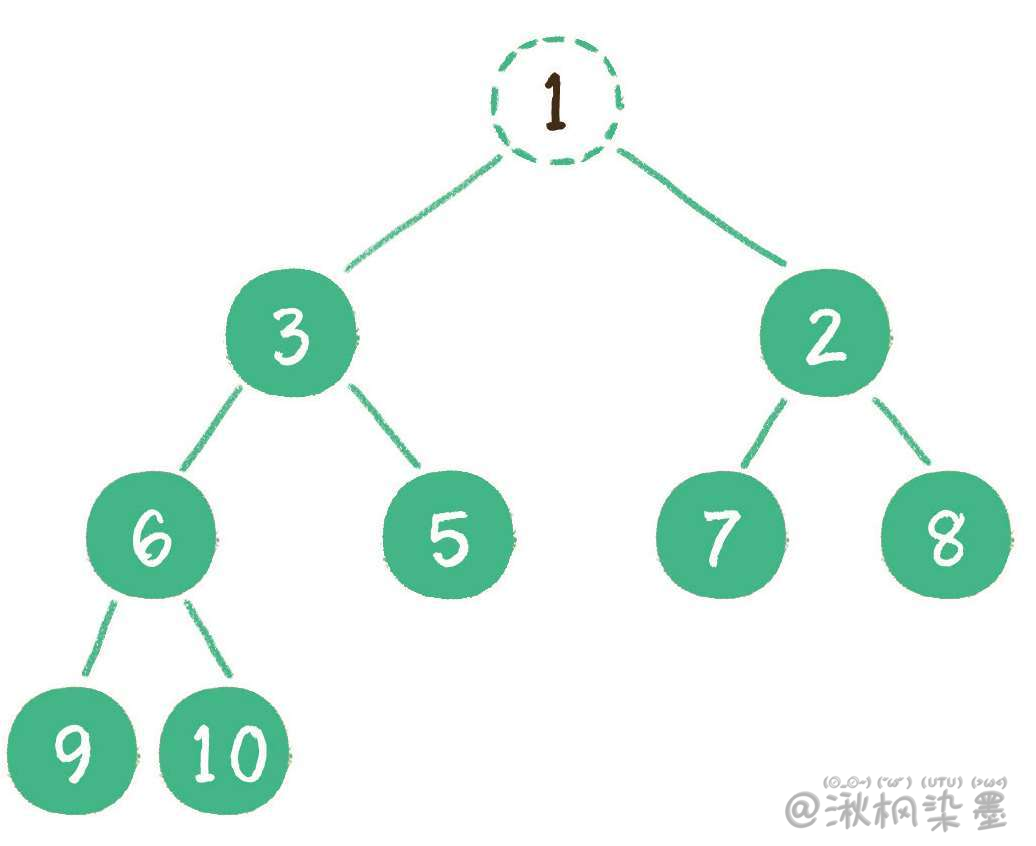
这时，为了继续维持完全二叉树的结构，我们把堆的最后一个节点10临时补到原本堆顶的位置。

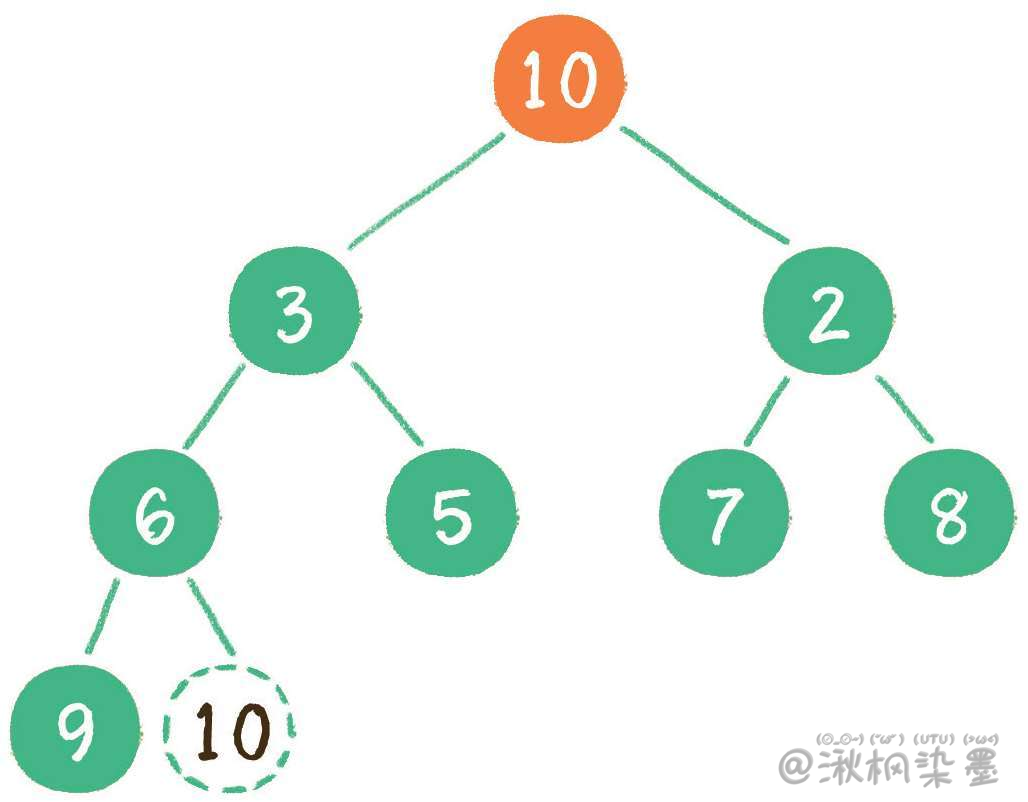
接下来，让暂处堆顶位置的节点10和它的左、右孩子进行比较，如果左、右孩子节点中最小的一个（显然是节点2）比节点10小，那么让节点10 "下沉"。

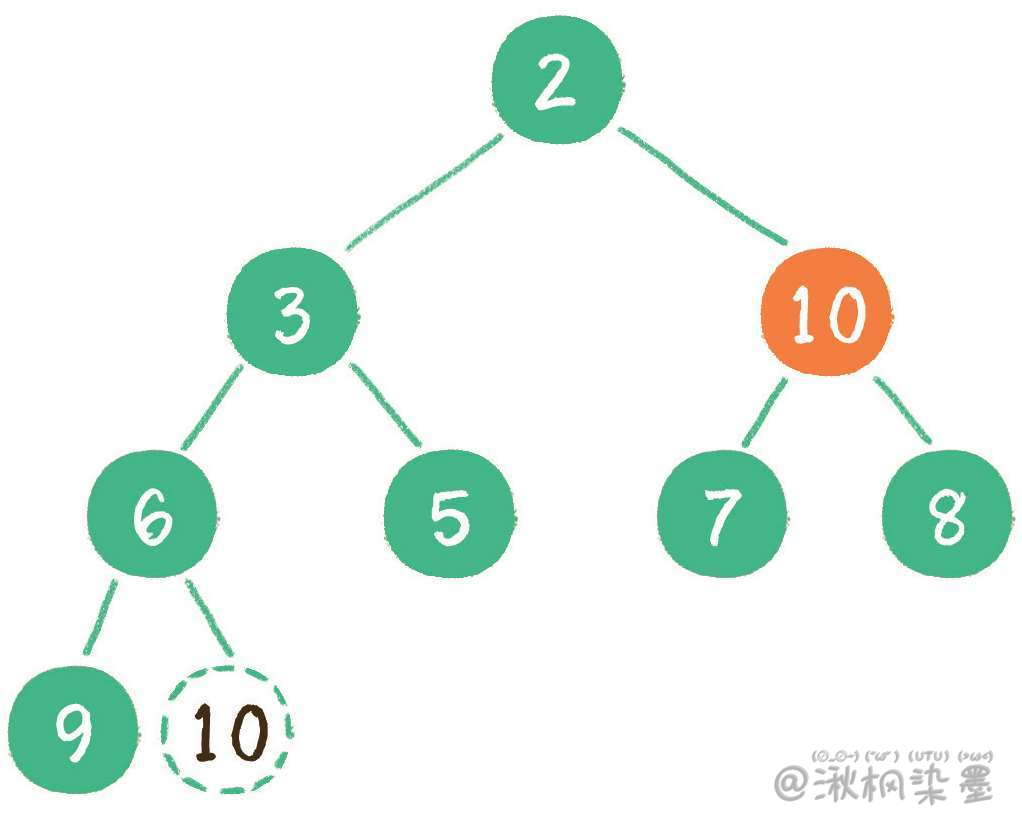
继续让节点10和它的左、右孩子做比较，左、右孩子中最小的是节点7，由于10大于7，让节点10继续 "下沉"。

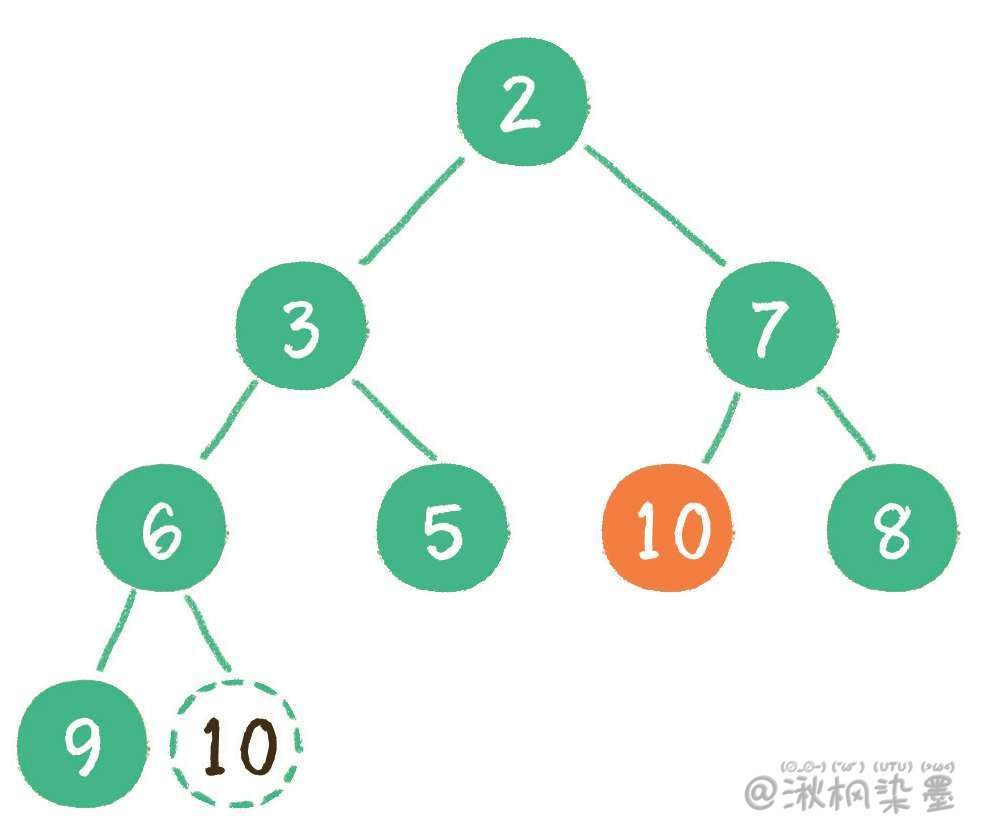
4.4 构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质就是让所有非叶子节点依次 "下沉"

下面举一个无序完全二叉树的例子，如下图所示。

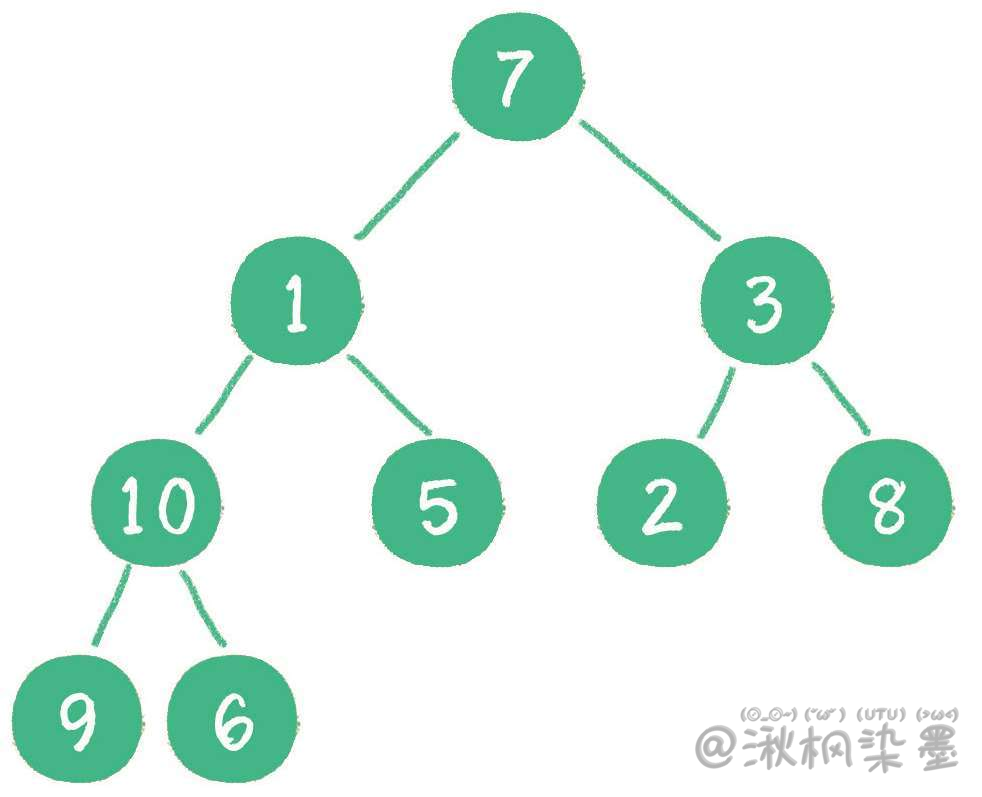
首先，从最后一个非叶子节点开始，也就是从节点10开始。如果节点10大于它左、右孩子节点中最小的一个，则节点10 "下沉"。

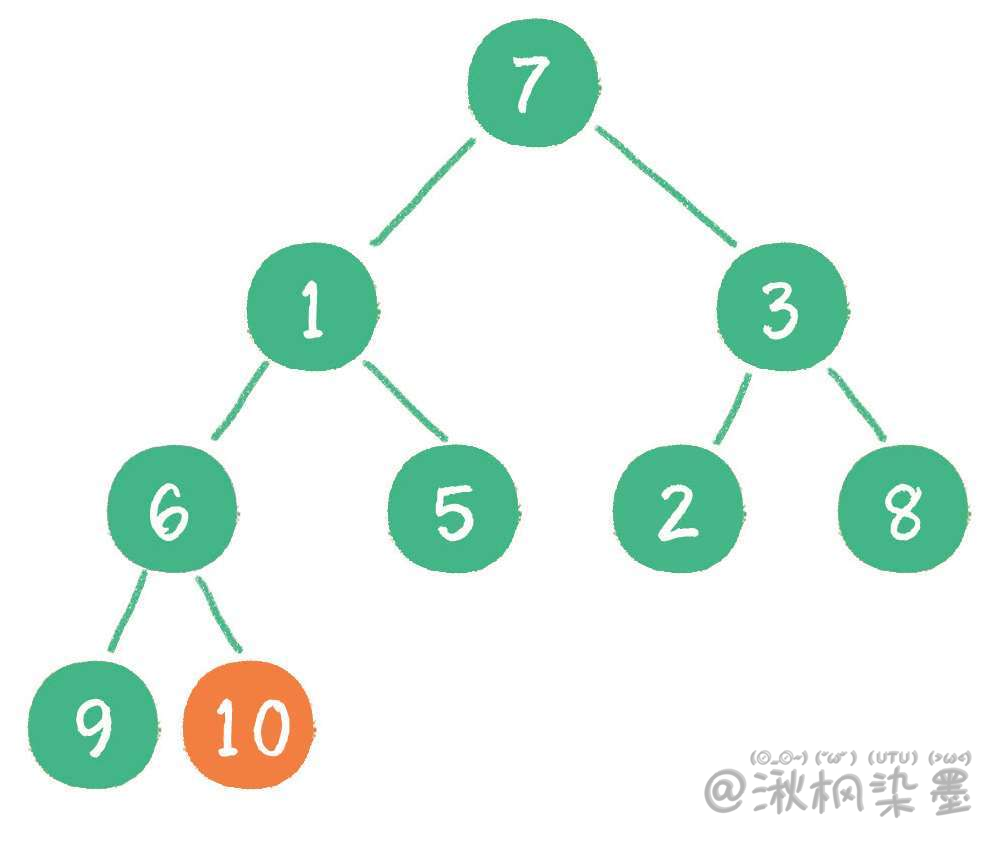
接下来轮到节点3，如果节点3大于它左、右孩子节点中最小的一个，则节点3“下沉”。

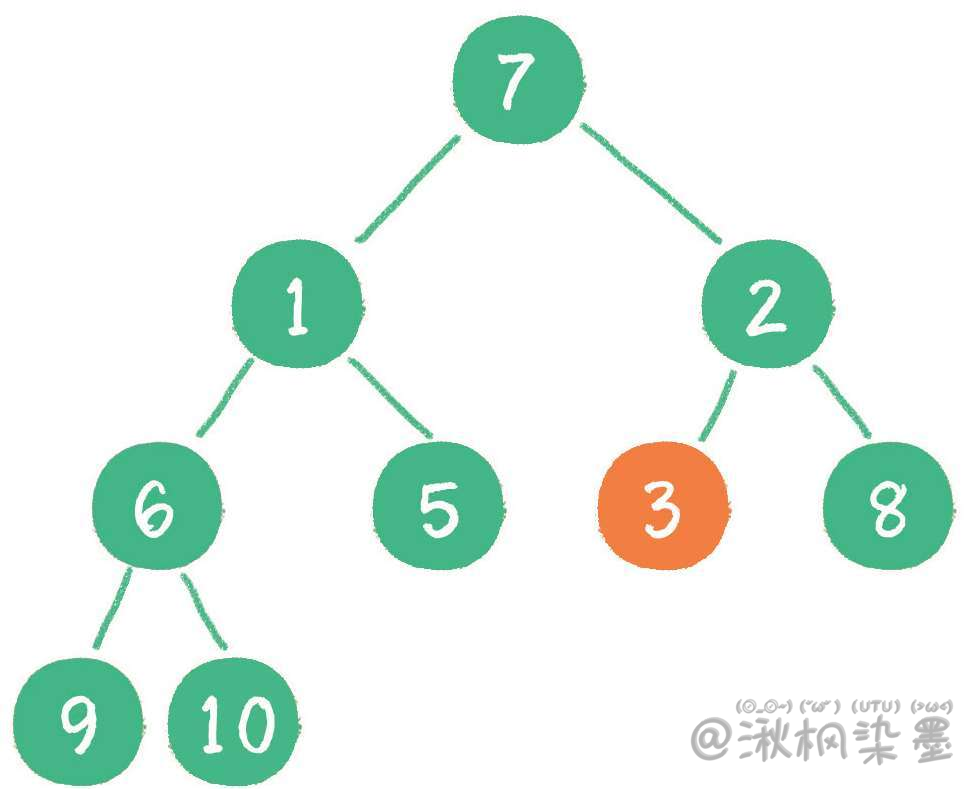
然后轮到节点1，如果节点1大于它左、右孩子节点中最小的一个，则节点1 "下沉"。事实上节点1小于它的左、右孩子，所以不用改变。

接下来轮到节点7，如果节点7大于它左、右孩子节点中最小的一个，则节点7 "下沉"。

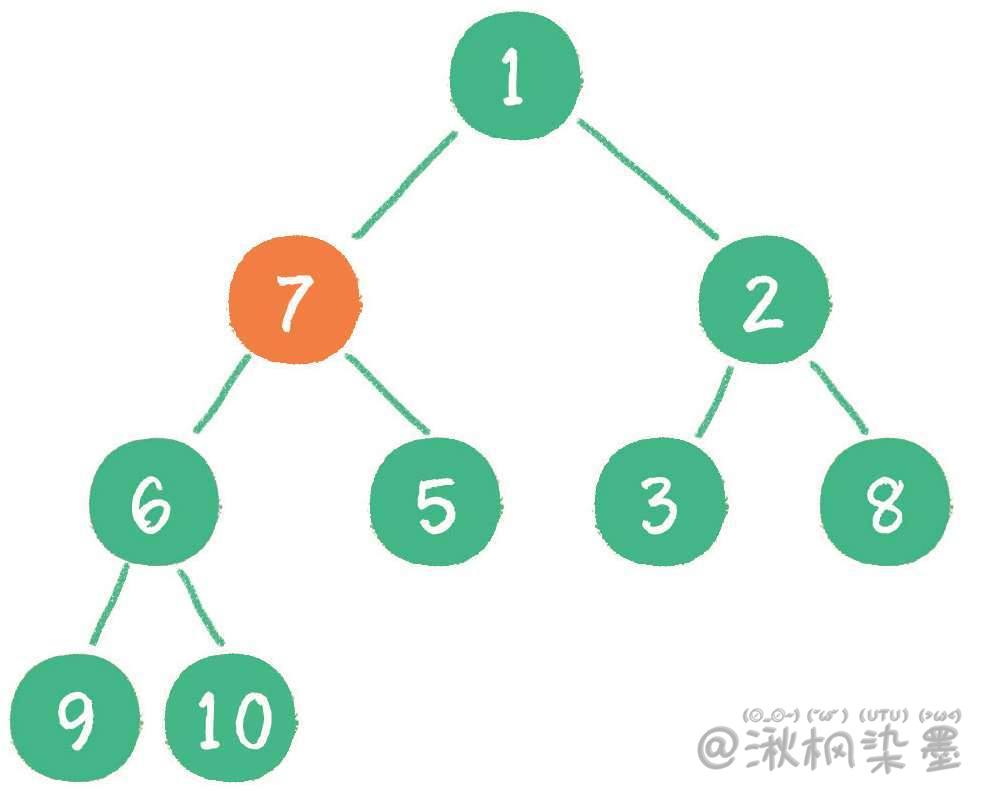
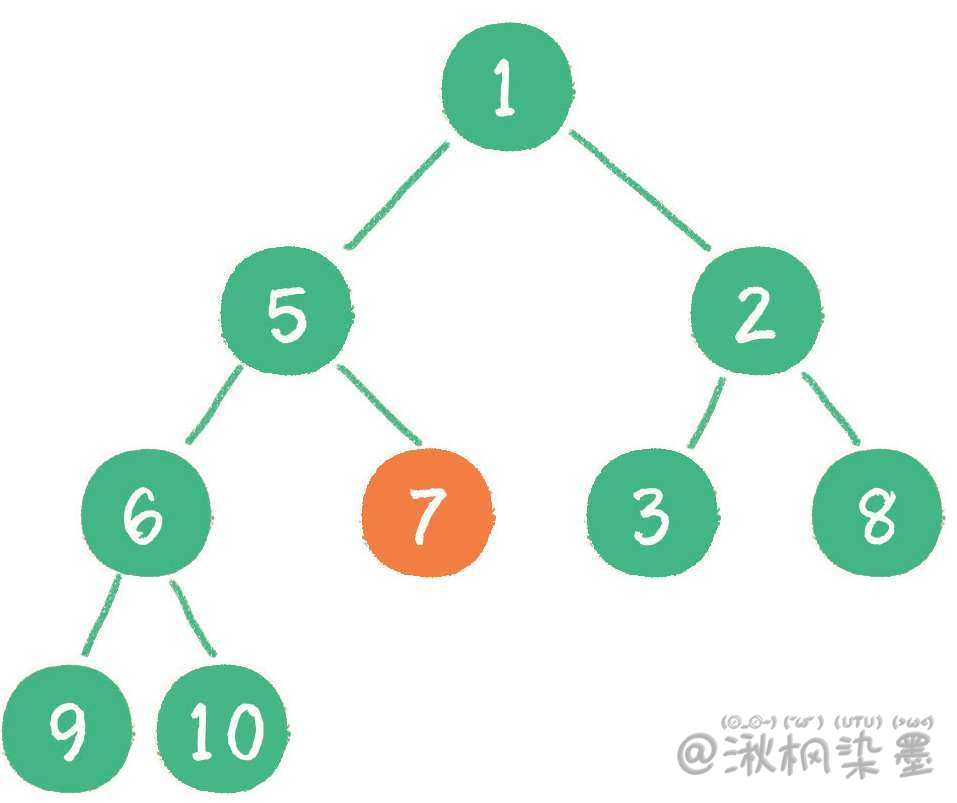
节点7继续比较，继续 "下沉"。

4.5 时间复杂度

操作	时间复杂度
插入节点	O(logn)
删除节点	O(logn)
构建二叉堆	O(n)

4.6 代码实现

二叉堆虽然是一个完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组中。

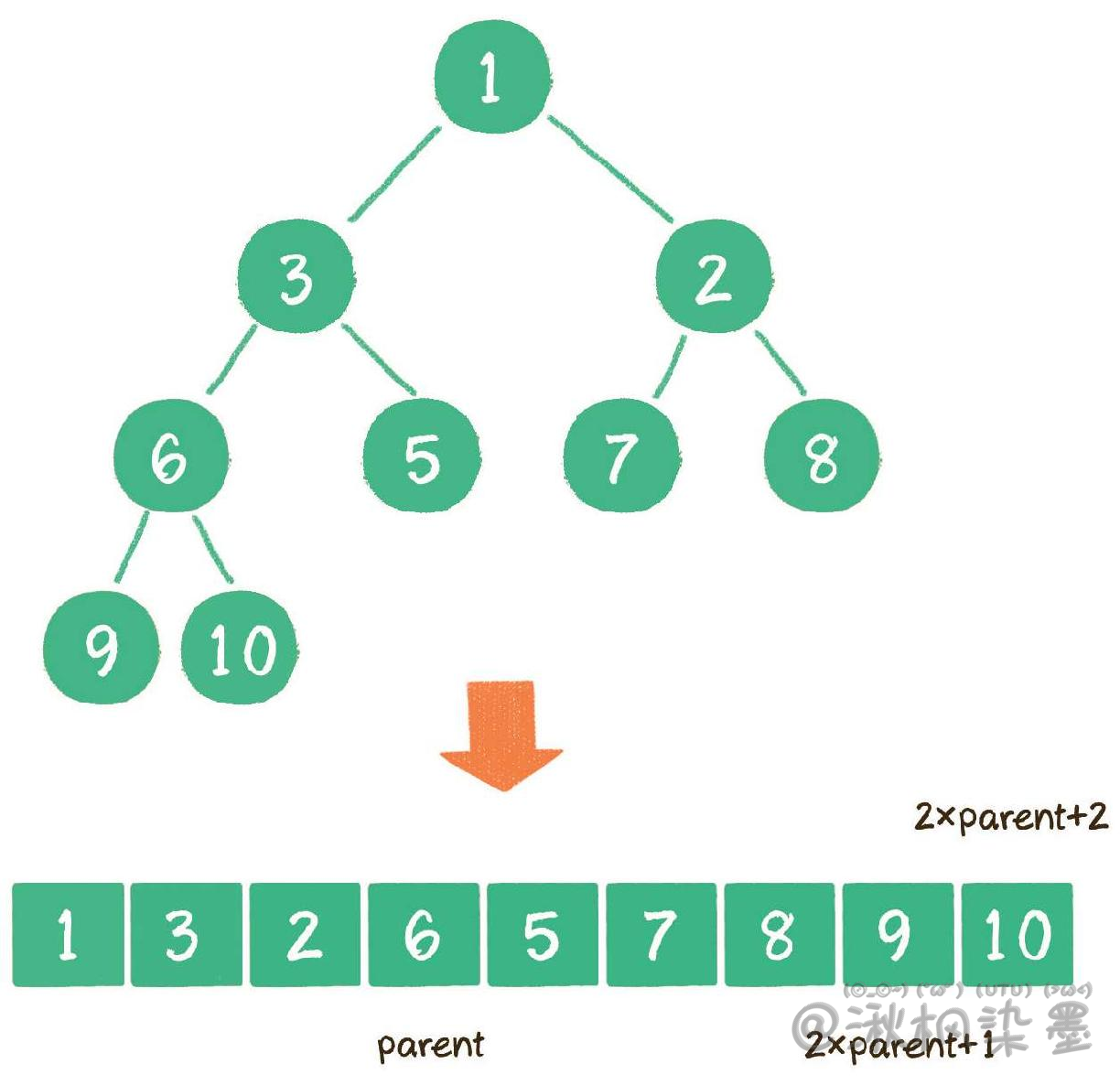
在数组中，在没有左、右指针的情况下，如何定位一个父节点的左孩子和右孩子呢？

像上图那样，可以依靠数组下标来计算。

假设父节点的下标是parent，那么它的左孩子下标就是 2×parent+1；右孩子下标就是 2×parent+2。

例如上面的例子中，节点6包含9和10两个孩子节点，节点6在数组中的下标是3，节点9在数组中的下标是7，节点10在数组中的下标是8。

那么，

7 = 3×2+1，

8 = 3×2+2，

public class BinaryHeap {

    /**
     * "上浮" 调整
     *
     * @param array 待调整的堆
     */
    public static void upAdjust(int[] array) {
        int childIndex = array.length - 1;
        int parentIndex = (childIndex - 1) / 2;
        // temp 保存插入的叶子节点值，用于最后的赋值
        int temp = array[childIndex];
        while (childIndex > 0 && temp < array[parentIndex]) {
            //无须真正交换，单向赋值即可
            array[childIndex] = array[parentIndex];
            childIndex = parentIndex;
            parentIndex = (parentIndex - 1) / 2;
        }
        array[childIndex] = temp;
    }

    /**
     * "下沉"调整
     *
     * @param array       待调整的堆
     * @param parentIndex 要"下沉"的父节点
     * @param length      堆的有效大小
     */
    public static void downAdjust(int[] array, int parentIndex, int length) {
        // temp 保存父节点值，用于最后的赋值
        int temp = array[parentIndex];
        int childIndex = 2 * parentIndex + 1;
        while (childIndex < length) {
            // 如果有右孩子，且右孩子小于左孩子的值，则定位到右孩子
            if (childIndex + 1 < length && array[childIndex + 1] <
                    array[childIndex]) {
                childIndex++;
            }
            // 如果父节点小于任何一个孩子的值，则直接跳出
            if (temp <= array[childIndex])
                break;
            //无须真正交换，单向赋值即可
            array[parentIndex] = array[childIndex];
            parentIndex = childIndex;
            childIndex = 2 * childIndex + 1;
        }
        array[parentIndex] = temp;
    }

    /**
     * 构建堆
     *
     * @param array 待调整的堆
     */
    public static void buildHeap(int[] array) {
        // 从最后一个非叶子节点开始，依次做"下沉"调整
        for (int i = (array.length - 2) / 2; i >= 0; i--) {
            downAdjust(array, i, array.length);
        }
    }

    public static void main(String[] args) {
        int[] array = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
        upAdjust(array);
        System.out.println(Arrays.toString(array));     // [0, 1, 2, 6, 3, 7, 8, 9, 10, 5]

        array = new int[]{7, 1, 3, 10, 5, 2, 8, 9, 6};
        buildHeap(array);
        System.out.println(Arrays.toString(array));     // [1, 5, 2, 6, 7, 3, 8, 9, 10]
    }

}

代码中有一个优化的点，就是在父节点和孩子节点做连续交换时，并不一定要真的交换，只需要先把交换一方的值存入temp变量，做单向覆盖，循环结束后，再把temp的值存入交换后的最终位置即可。

二叉堆是实现堆排序及优先队列的基础。

五：优先队列

优先队列不再遵循先入先出的原则，而是分为两种情况。

• 最大优先队列，无论入队顺序如何，都是当前最大的元素优先出队；
• 最小优先队列，无论入队顺序如何，都是当前最小的元素优先出队。

要实现以上需求，利用线性数据结构并非不能实现，但是时间复杂度较高。这时候二叉堆就派上用场了。

每一次入队操作就是堆的插入操作，每一次出队操作就是删除堆顶节点。

5.1 入队

插入新节点5。

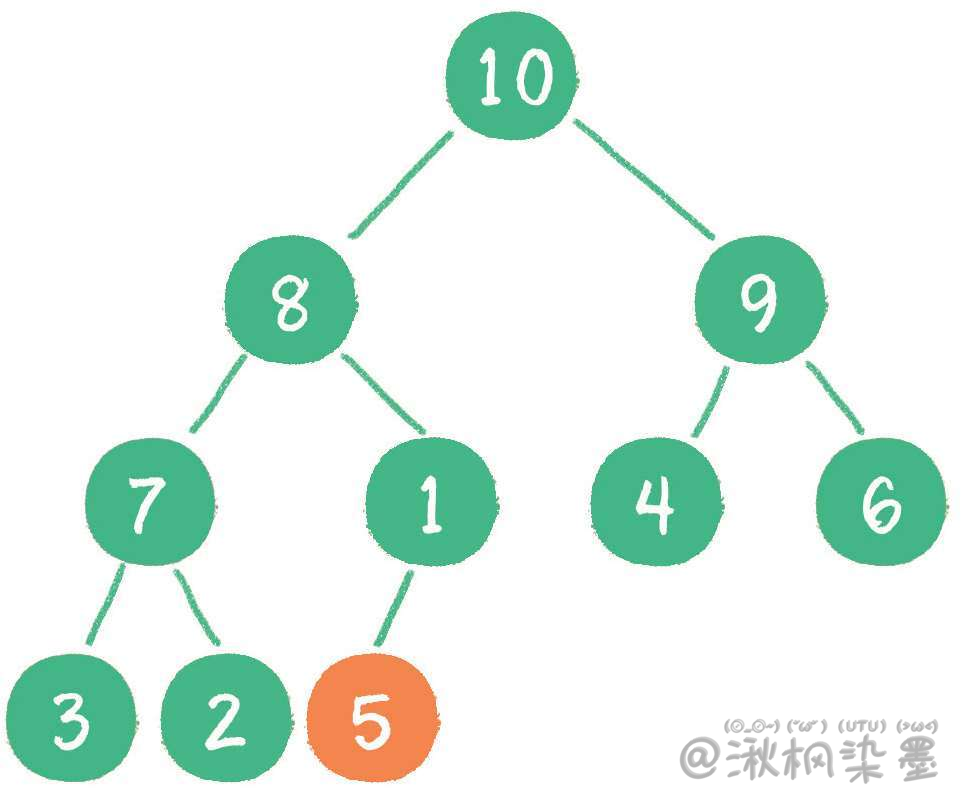
新节点5"上浮"到合适位置。

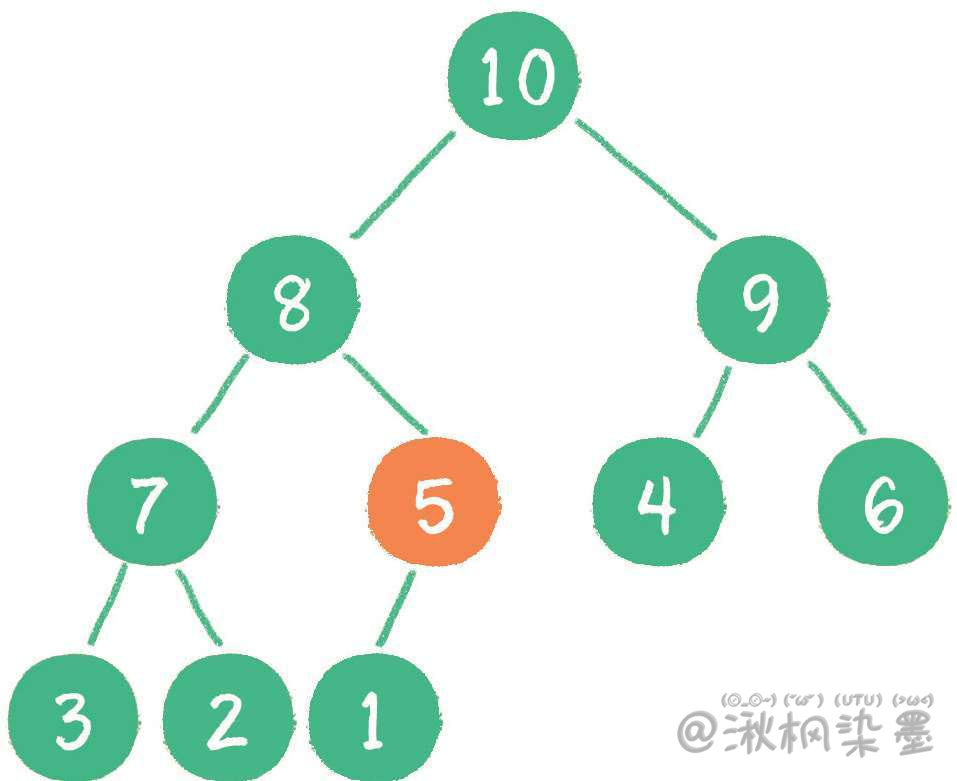
5.2 出队

让原堆顶节点10出队。

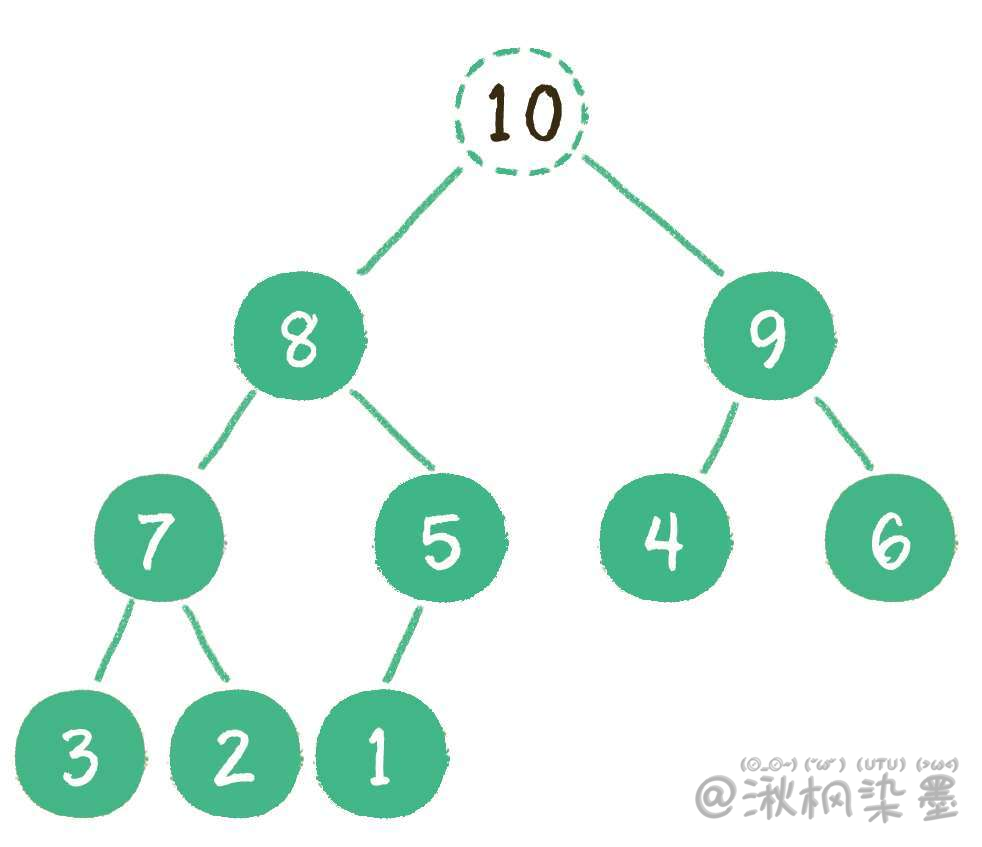
把最后一个节点1替换到堆顶位置。

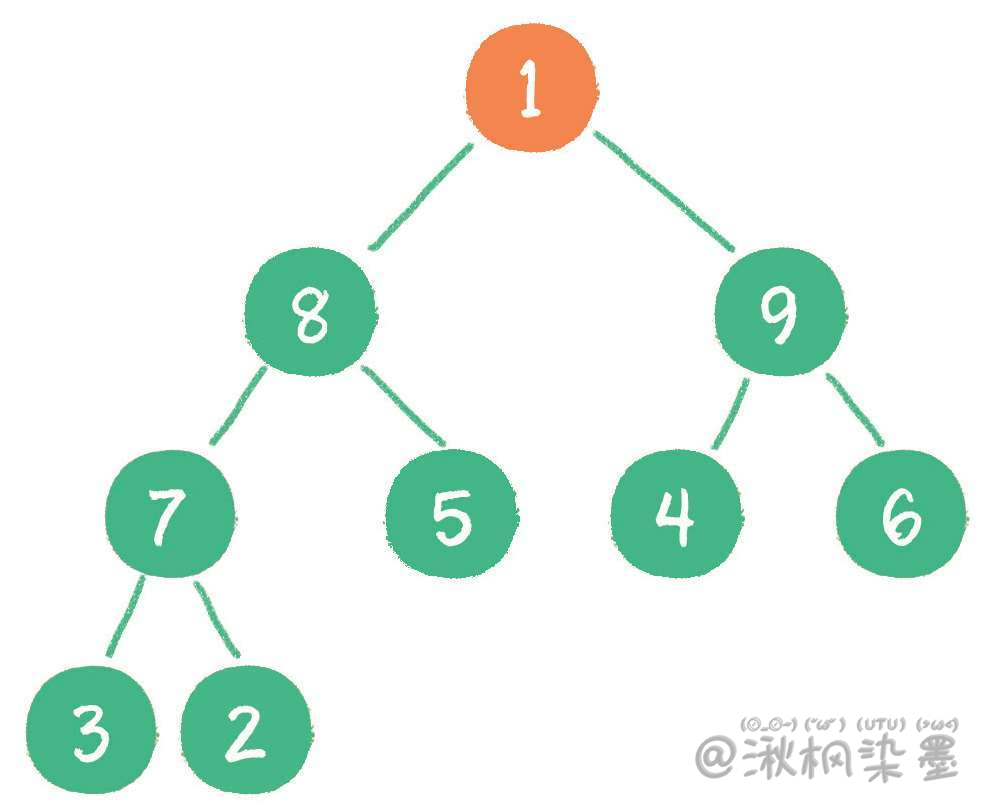
节点1"下沉"，节点9成为新堆顶。

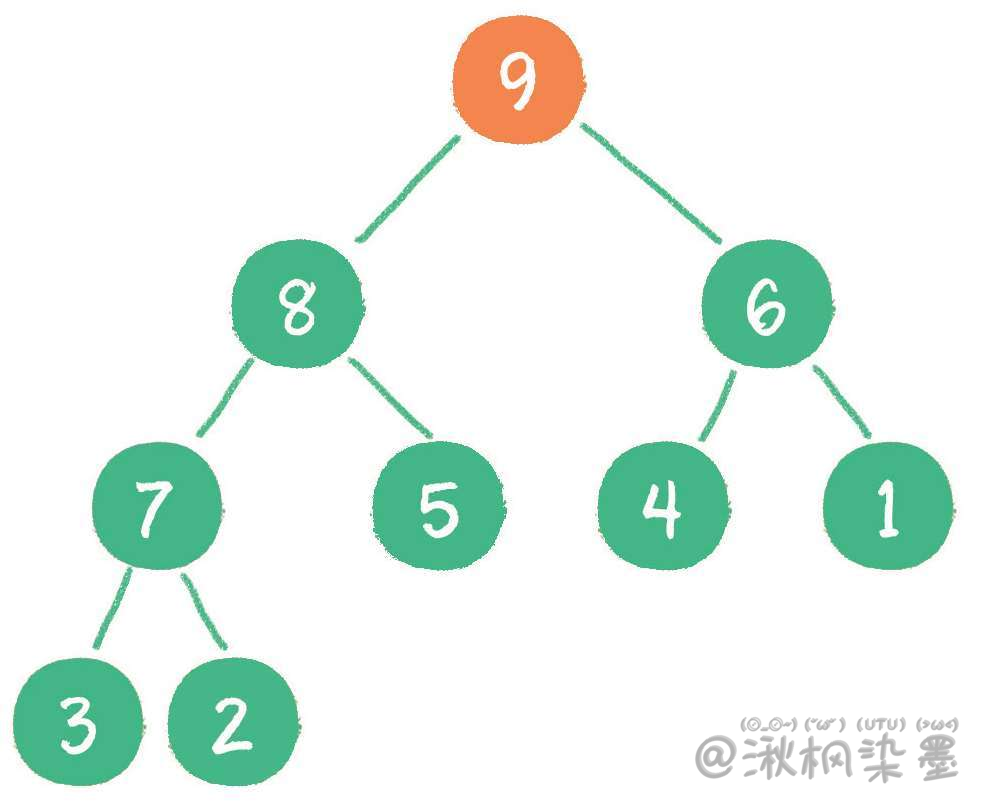
5.3 时间复杂度

操作	时间复杂度
入队	O(logn)
出队	O(logn)

5.4 代码实现

public class PriorityQueue {

    private int[] array;
    private int size;

    public PriorityQueue() {
        // 队列初始长度为32
        array = new int[32];
    }

    /**
     * 入队
     *
     * @param key 入队元素
     */
    public void enQueue(int key) {
        // 队列长度超出范围，扩容
        if (size >= array.length) {
            resize();
        }
        array[size++] = key;
        upAdjust();
    }

    /**
     * 出队
     */
    public int deQueue() throws Exception {
        if (size <= 0) {
            throw new Exception("the queue is empty !");
        }
        // 获取堆顶元素
        int head = array[0];
        // 让最后一个元素移动到堆顶
        array[0] = array[--size];
        downAdjust();
        return head;
    }

    /**
     * “上浮”调整
     */
    private void upAdjust() {
        int childIndex = size - 1;
        int parentIndex = (childIndex - 1) / 2;
        // temp 保存插入的叶子节点值，用于最后的赋值
        int temp = array[childIndex];
        while (childIndex > 0 && temp > array[parentIndex]) {
            // 无须真正交换，单向赋值即可
            array[childIndex] = array[parentIndex];
            childIndex = parentIndex;
            parentIndex = parentIndex / 2;
        }
        array[childIndex] = temp;
    }

    /**
     * “下沉”调整
     */
    private void downAdjust() {
        // temp 保存父节点的值，用于最后的赋值
        int parentIndex = 0;
        int temp = array[parentIndex];
        int childIndex = 1;
        while (childIndex < size) {
            //  如果有右孩子，且右孩子大于左孩子的值，则定位到右孩子
            if (childIndex + 1 < size && array[childIndex + 1] >
                    array[childIndex]) {
                childIndex++;
            }
            // 如果父节点大于任何一个孩子的值，直接跳出
            if (temp >= array[childIndex])
                break;
            // 无须真正交换，单向赋值即可
            array[parentIndex] = array[childIndex];
            parentIndex = childIndex;
            childIndex = 2 * childIndex + 1;
        }
        array[parentIndex] = temp;
    }

    /**
     * 队列扩容
     */
    private void resize() {
        // 队列容量翻倍
        int newSize = this.size * 2;
        this.array = Arrays.copyOf(this.array, newSize);
    }

    public static void main(String[] args) throws Exception {
        PriorityQueue priorityQueue = new PriorityQueue();
        priorityQueue.enQueue(3);
        priorityQueue.enQueue(5);
        priorityQueue.enQueue(10);
        priorityQueue.enQueue(2);
        priorityQueue.enQueue(7);
        System.out.println("出队元素：" + priorityQueue.deQueue());  // 出队元素：10
        System.out.println("出队元素：" + priorityQueue.deQueue());  // 出队元素：7
    }
}

上述代码采用数组来存储二叉堆的元素，因此当元素数量超过数组长度时，需要进行扩容来扩大数组长度。

五：参考文献

• 《大话数据结构 — 程杰》
• 《漫画算法 — 魏梦舒》